Abstract cell complex, Abstract type, Closure (mathematics)

सार सेल जटिल: गणितमा, एउटा एब्स्ट्र्याक्ट सेल जटिल एउटा अब्स्ट्र्याक्ट सेट छ अलेक्जान्ड्रोभ टोपोलॉजीको साथ, जहाँ आयाम भनिने गैर-negativeणात्मक पूर्णांक संख्या प्रत्येक पोइन्टमा तोकिएको हुन्छ। जटिललाई "अमूर्त" भनिन्छ किनकि यसको पोइन्टहरू, जसलाई "कक्षहरू" भनिन्छ, हाउस्डर्फ स्पेसको उपसमेत होइन किनकि यो युक्लिडियन र सीडब्ल्यू जटिलमा रहेको छ। एब्स्ट्र्याक्ट सेल जटिलहरूले छवि विश्लेषण र कम्प्युटर ग्राफिक्समा महत्त्वपूर्ण भूमिका खेल्दछ।
सार प्रकार: प्रोग्रामि languages ​​भाषाहरूमा, एउटा एब्स्ट्र्याक्ट प्रकार एक नामनिर्देशन प्रणालीमा एक प्रकार हो जुन सीधा स्थापित हुन सक्दैन; एक प्रकार जुन एब्स्ट्र्याक्ट छैन - जुन इन्स्ट्यान्ट गर्न सकिन्छ - यसलाई क concrete्क्रीट प्रकार भनिन्छ । अमूर्त प्रकारको प्रत्येक उदाहरण केही क some्क्रीट उपप्रकारको उदाहरण हो। अमूर्त प्रकारहरू अस्तित्वगत प्रकारहरू पनि भनेर चिनिन्छन्।
बन्द (गणित): गणितमा, सेट अपरेसन अन्तर्गत बन्द हुन्छ यदि सेटको सदस्यहरूमा त्यो अपरेशन प्रदर्शन गर्दै सधै त्यस सेटको सदस्य उत्पन्न गर्दछ। उदाहरण को लागी, धनात्मक पूर्णा under्क थपको अन्तमा बन्द हुन्छ, तर घटाउ अन्तर्गत होइन: १ - २ सकारात्मक पूर्णांक होईन जबकि दुबै १ र २ सकारात्मक पूर्णांक हुन्। अर्को उदाहरण सेट मात्र शून्य, जो थप, घटाउ र गुणन अन्तर्गत बन्द छ।
बन्द (गणित): गणितमा, सेट अपरेसन अन्तर्गत बन्द हुन्छ यदि सेटको सदस्यहरूमा त्यो अपरेशन प्रदर्शन गर्दै सधै त्यस सेटको सदस्य उत्पन्न गर्दछ। उदाहरण को लागी, धनात्मक पूर्णा under्क थपको अन्तमा बन्द हुन्छ, तर घटाउ अन्तर्गत होइन: १ - २ सकारात्मक पूर्णांक होईन जबकि दुबै १ र २ सकारात्मक पूर्णांक हुन्। अर्को उदाहरण सेट मात्र शून्य, जो थप, घटाउ र गुणन अन्तर्गत बन्द छ।
अमूर्त हास्य एब्स्ट्र्याक्ट कमिक्स हास्य हास्य हुन् जसले दृश्य एब्स्ट्र्यासनको अवधारणालाई हास्य स्ट्रिपको परम्परागत निरन्तरतासँग मिलाउँछ।
सार मेशिन: एउटा एब्स्ट्र्याक्ट मेशिन , जसलाई एब्स्ट्र्याक्ट कम्प्यूटर पनि भनिन्छ, एक सैद्धांतिक कम्प्युटर हो जुन गणनाको मोडेल परिभाषित गर्न प्रयोग गरिन्छ। कम्प्युटि processes प्रक्रियाहरूको एब्स्ट्र्यासन दुबै कम्प्युटर विज्ञान र कम्प्युटर ईन्जिनियरि discip विषयहरूमा प्रयोग गरिन्छ र सामान्यतया एक असक्रिय समय प्रतिमान ग्रहण गर्दछ।
अवधारणा: अवधारणाहरू अमूर्त विचारहरू वा दिमाग, भाषण, वा विचारमा हुने सामान्य धारणाको रूपमा परिभाषित गरिन्छ। तिनीहरू विचार र विश्वासको आधारभूत निर्माण ब्लक हो भनेर बुझिन्छ। तिनीहरू अनुभूतिको सबै पक्षहरूमा महत्त्वपूर्ण भूमिका खेल्छन्। त्यस्तै, भाषाहरू, मनोविज्ञान, र दर्शन जस्ता धेरै विषयहरू द्वारा अवधारणाहरूको अध्ययन गरिन्छ, र यी विषयहरूमा अवधारणाहरूको तार्किक र मनोवैज्ञानिक संरचनामा चासो राख्दछन्, र कसरी उनीहरू विचार र वाक्यहरू गठन गर्न सँगै राखिन्छन्। अवधारणाको अध्ययनले उदीयमान अन्तःविषय दृष्टिकोणको महत्त्वपूर्ण फ्लगशिपको रूपमा काम गरेको छ जसलाई संज्ञानात्मक विज्ञान भनिन्छ।
सारांश: यसको मुख्य अर्थमा एब्स्ट्र्याक्सन एक वैचारिक प्रक्रिया हो जहाँ सामान्य नियमहरू र अवधारणाहरू विशिष्ट उदाहरणहरूको शाब्दिक अर्थ, पहिलो सिद्धान्त, वा अन्य विधिहरूको प्रयोग र वर्गीकरणबाट लिइएको हो।
एब्स्ट्र्याक्ट डाटा प्रकार: कम्प्युटर विज्ञानमा, एउटा अमूर्त डाटा प्रकार ( ADT ) डाटा प्रकारका लागि गणितिय मोडेल हो। एउटा अमूर्त डाटा प्रकार यसको व्यवहार (शब्दार्थ) द्वारा एक प्रयोगकर्ता , डाटाको दृष्टिकोणबाट परिभाषित गरिएको छ विशेष गरी सम्भव मानको सर्तमा, यस प्रकारको डाटामा सम्भावित अपरेशनहरू, र यी अपरेशनहरूको व्यवहारबाट। यो गणितिय मोडेल डाटा संरचनासँग भिन्न छ जुन डाटाको ठोस प्रतिनिधित्व हो, र लागूकर्ताको दृष्टिकोण हो, प्रयोगकर्ता होईन।
एब्स्ट्र्याक्ट डाटा प्रकार: कम्प्युटर विज्ञानमा, एउटा अमूर्त डाटा प्रकार ( ADT ) डाटा प्रकारका लागि गणितिय मोडेल हो। एउटा अमूर्त डाटा प्रकार यसको व्यवहार (शब्दार्थ) द्वारा एक प्रयोगकर्ता , डाटाको दृष्टिकोणबाट परिभाषित गरिएको छ विशेष गरी सम्भव मानको सर्तमा, यस प्रकारको डाटामा सम्भावित अपरेशनहरू, र यी अपरेशनहरूको व्यवहारबाट। यो गणितिय मोडेल डाटा संरचनासँग भिन्न छ जुन डाटाको ठोस प्रतिनिधित्व हो, र लागूकर्ताको दृष्टिकोण हो, प्रयोगकर्ता होईन।
एब्स्ट्र्याक्ट डाटा प्रकार: कम्प्युटर विज्ञानमा, एउटा अमूर्त डाटा प्रकार ( ADT ) डाटा प्रकारका लागि गणितिय मोडेल हो। एउटा अमूर्त डाटा प्रकार यसको व्यवहार (शब्दार्थ) द्वारा एक प्रयोगकर्ता , डाटाको दृष्टिकोणबाट परिभाषित गरिएको छ विशेष गरी सम्भव मानको सर्तमा, यस प्रकारको डाटामा सम्भावित अपरेशनहरू, र यी अपरेशनहरूको व्यवहारबाट। यो गणितिय मोडेल डाटा संरचनासँग भिन्न छ जुन डाटाको ठोस प्रतिनिधित्व हो, र लागूकर्ताको दृष्टिकोण हो, प्रयोगकर्ता होईन।
एब्स्ट्र्याक्ट डाटा प्रकार: कम्प्युटर विज्ञानमा, एउटा अमूर्त डाटा प्रकार ( ADT ) डाटा प्रकारका लागि गणितिय मोडेल हो। एउटा अमूर्त डाटा प्रकार यसको व्यवहार (शब्दार्थ) द्वारा एक प्रयोगकर्ता , डाटाको दृष्टिकोणबाट परिभाषित गरिएको छ विशेष गरी सम्भव मानको सर्तमा, यस प्रकारको डाटामा सम्भावित अपरेशनहरू, र यी अपरेशनहरूको व्यवहारबाट। यो गणितिय मोडेल डाटा संरचनासँग भिन्न छ जुन डाटाको ठोस प्रतिनिधित्व हो, र लागूकर्ताको दृष्टिकोण हो, प्रयोगकर्ता होईन।
एब्स्ट्र्याक्ट डाटा प्रकार: कम्प्युटर विज्ञानमा, एउटा अमूर्त डाटा प्रकार ( ADT ) डाटा प्रकारका लागि गणितिय मोडेल हो। एउटा अमूर्त डाटा प्रकार यसको व्यवहार (शब्दार्थ) द्वारा एक प्रयोगकर्ता , डाटाको दृष्टिकोणबाट परिभाषित गरिएको छ विशेष गरी सम्भव मानको सर्तमा, यस प्रकारको डाटामा सम्भावित अपरेशनहरू, र यी अपरेशनहरूको व्यवहारबाट। यो गणितिय मोडेल डाटा संरचनासँग भिन्न छ जुन डाटाको ठोस प्रतिनिधित्व हो, र लागूकर्ताको दृष्टिकोण हो, प्रयोगकर्ता होईन।
सार कला: अमूर्त कलाले आकार, फार्म, रंग र रेखाको दृश्य भाषा प्रयोग गर्दछ रचना सिर्जना गर्न जुन विश्वमा दृश्य सन्दर्भहरूबाट स्वतन्त्रताको डिग्रीको साथ अवस्थित हुन सक्छ। पश्चिमी कला १ th औं शताब्दीको बीचमा नवजागरणदेखि मध्य परिप्रेक्ष्यमा थियो, परिप्रेक्ष्यको तर्क र दृश्यता वास्तविकताको भ्रम पुनः उत्पन्न गर्ने प्रयासले समेट्यो। १ th औं शताब्दीको अन्तसम्ममा धेरै कलाकारहरूले नयाँ किसिमको कला सिर्जना गर्ने आवश्यकता महसुस गरे जुन टेक्नोलोजी, विज्ञान र दर्शनमा हुने मौलिक परिवर्तनहरूलाई समेट्ने थियो। स्रोतबाट व्यक्ति कलाकारहरूले उनीहरूको सैद्धांतिक तर्कहरू विविध थिए, र त्यो समयको पश्चिमी संस्कृतिको सबै क्षेत्रमा सामाजिक र बौद्धिक व्याकुलता प्रतिबिम्बित गर्दछ।
सार र ठोस: मेटाफिजिक्समा अमूर्त र कंक्रीट बीचको भिन्नता दुई प्रकारका निकायहरू बीचको विभाजनलाई जनाउँछ। धेरै दार्शनिकहरू भन्छन कि यो भिन्नताको मौलिक मेटाफिजिकल महत्त्व छ। कंक्रीट वस्तुहरूका उदाहरणहरूमा बोटबिरुवा, मानव र ग्रहहरू समावेश छन् जबकि चीजहरू संख्या, सेट र प्रस्तावहरू अमूर्त वस्तुहरू हुन् । संक्षिप्तता र अमूर्तताको चरित्रको चिह्न के हो भन्ने बारे कुनै सहमति छैन। लोकप्रिय सुझावहरूले अन्तरिक्षको बीचमा अन्तर छुट्याउने समावेश गर्दछ (१) अन्तरिक्ष समय भित्र वा बाहिर अवस्थित, (२) कारण र प्रभावहरू हुनु वा नहुनु, ()) आकस्मिक वा आवश्यक अस्तित्व हुनु, ()) विशेष वा विश्वव्यापी हुनु र ()) या त शारीरिक वा मानसिक क्षेत्र बाट सम्बन्धित छ। दृष्टिकोणको यस विविधताको बावजुद, प्रायः वस्तुहरूको बारेमा विस्तृत सम्झौता छ कि तिनीहरू अमूर्त वा क concreteक्रीट हुन्। त्यसोभए प्रायः व्याख्याहरूको अन्तर्गत, यी सबै विचारहरू सहमत हुनेछन्, उदाहरणका लागि, बोटहरू ठोस वस्तुहरू हुन् जबकि संख्याहरू अमूर्त वस्तुहरू हुन्छन्।
सार भिन्न भिन्न समीकरण: गणितमा, एउटा अमूर्त विभेदक समीकरण भिन्न भिन्न समीकरण हो जहाँ अज्ञात प्रकार्य र यसका डेरिभेटिभहरूले केही सामान्य सारमा स्थान लिन्छन्। यस प्रकारका समीकरणहरू आंशिक विभेदक समीकरणहरूको अध्ययनमा उदाउँदछन्: यदि कुनै एउटा चरलाई विशेषाधिकार दिइएको हुन्छ र अरू सबै एकसाथ राखिन्छन् भने, चरको सन्दर्भमा एक साधारण "भिन्न" समीकरण जुन प्रमाणमा राखिएको थियो। प्राप्त सीमा सर्तहरू थप्नाले प्राय: केही सुविधाजनक प्रकार्य खाली ठाउँहरूमा समाधानहरू विचार गर्ने ठाउँमा अनुवाद गर्न सकिन्छ।
सार विभेदक ज्यामिति: विशेषण अमूर्त प्राय: पहिले विभेदक ज्यामितिमा पहिले पनि प्रयोग गरिएको थियो, तर यस लेखको अमूर्त विभेदक ज्यामिति (एडीजी) चिकनाईको क्यालकुलस धारणाबिना भिन्न भिन्न ज्यामितिको एक रूप हो, जुन १ 1998 1998 from पछि अनास्तासियोस मल्लियोस र इओनिस रैप्टिसले विकास गरेका थिए।
गतिशील प्रणाली र भिन्न समीकरण शीर्षकहरूको सूची: यो विकिपेडिया पृष्ठ द्वारा गतिशील प्रणाली र भिन्न समीकरण शीर्षकहरूको सूची हो । आंशिक विभेदक समीकरण विषयहरूको सूची, समीकरणहरूको सूची पनि हेर्नुहोस्।
अमूर्त अर्थव्यवस्था: सैद्धान्तिक अर्थशास्त्रमा, एउटा अमूर्त अर्थतन्त्र भनेको एक मोडल हो जुन सूक्ष्म आर्थिकशास्त्रमा विनिमय अर्थव्यवस्थाको मानक मोडल र खेल सिद्धान्तमा खेलको मानक मोडेल दुवैलाई सामान्यीकरण गर्दछ। एक अमूर्त अर्थव्यवस्था मा एक संतुलन सुक्ष्मअर्थशास्त्र मा एक Walrasian संतुलन, र खेल-सिद्धान्त मा एक नैश संतुलन दुवै generalizes।
सार प्राथमिक वर्ग: नमूना सिद्धान्तमा, गणित तर्कको भित्र एउटा अनुशासन, एउटा अमूर्त प्राथमिक वर्ग , वा छोटको लागि एईसी , मोडलहरूको वर्ग हो जुन आंशिक अर्डरको साथ पहिलो अर्डर मोडल सिद्धान्तमा प्राथमिक वर्गको प्राथमिक संरचनाको सम्बन्धसँग मिल्दोजुल्दो हुन्छ। उनीहरु सहारोन शेलाले परिचय दिएका थिए।
ईम्बेडिंग: गणितमा, एम्बेडिding भनेको अर्को गणित संरचनाको एक उदाहरण हो जुन अर्को उदाहरणमा समाहित हुन्छ, जस्तै समूह जुन सबसमूह हो।
समाजशास्त्रीय कल्पना: समाजशास्त्रीय कल्पना १ 195 9 book को अमेरिकी समाजशास्त्री सी। राइट मिल्सले अक्सफोर्ड युनिभर्सिटी प्रेस द्वारा प्रकाशित पुस्तक हो। यसमा उनले समाजशास्त्रीय कल्पनाको विचार विकास गर्दछन्, जुन माध्यमबाट आत्म र समाजको बीचमा सम्बन्ध बुझ्न सकिन्छ।
सार र ठोस: मेटाफिजिक्समा अमूर्त र कंक्रीट बीचको भिन्नता दुई प्रकारका निकायहरू बीचको विभाजनलाई जनाउँछ। धेरै दार्शनिकहरू भन्छन कि यो भिन्नताको मौलिक मेटाफिजिकल महत्त्व छ। कंक्रीट वस्तुहरूका उदाहरणहरूमा बोटबिरुवा, मानव र ग्रहहरू समावेश छन् जबकि चीजहरू संख्या, सेट र प्रस्तावहरू अमूर्त वस्तुहरू हुन् । संक्षिप्तता र अमूर्तताको चरित्रको चिह्न के हो भन्ने बारे कुनै सहमति छैन। लोकप्रिय सुझावहरूले अन्तरिक्षको बीचमा अन्तर छुट्याउने समावेश गर्दछ (१) अन्तरिक्ष समय भित्र वा बाहिर अवस्थित, (२) कारण र प्रभावहरू हुनु वा नहुनु, ()) आकस्मिक वा आवश्यक अस्तित्व हुनु, ()) विशेष वा विश्वव्यापी हुनु र ()) या त शारीरिक वा मानसिक क्षेत्र बाट सम्बन्धित छ। दृष्टिकोणको यस विविधताको बावजुद, प्रायः वस्तुहरूको बारेमा विस्तृत सम्झौता छ कि तिनीहरू अमूर्त वा क concreteक्रीट हुन्। त्यसोभए प्रायः व्याख्याहरूको अन्तर्गत, यी सबै विचारहरू सहमत हुनेछन्, उदाहरणका लागि, बोटहरू ठोस वस्तुहरू हुन् जबकि संख्याहरू अमूर्त वस्तुहरू हुन्छन्।
अस्तित्ववाद: अस्तित्ववाद (वा) दार्शनिक अनुसन्धानको एक रूप हो जुन मानव अस्तित्वको समस्या पत्ता लगाउँदछ र सोच्ने, अनुभव गर्ने, व्यक्तिको अभिनय गर्नेको जीवित अनुभवमा केन्द्रित हुन्छ। अस्तित्ववादीको दृष्टिकोणमा, व्यक्तिको सुरूवात विन्दुलाई "अस्तित्वगत एन्जास्ट" भनिएको छ, स्पष्ट रूपमा अर्थहीन वा बेतुका संसारको सामना गर्नुपर्दा डर, विचलित, भ्रम, वा चिन्ताको भाव। अस्तित्ववादी चिन्तकहरूले बारम्बार मानव अस्तित्वको अर्थ, उद्देश्य र मूल्यसँग सम्बन्धित मुद्दाहरूको अन्वेषण गर्दछन्।
सार अभिव्यक्तिवाद: अमूर्त अभिव्यक्तिवाद एक पोष्ट हो - अमेरिकी चित्रकलामा दोस्रो विश्व युद्ध कला आन्दोलन, १ 40 .० को दशकमा न्यू योर्कमा विकसित भयो। यो पहिलो विशेष गरी अमेरिकी अभियान हो जसले अन्तर्राष्ट्रिय प्रभाव प्राप्त गर्‍यो र न्यू योर्क शहरलाई पश्चिमी कला विश्वको केन्द्रमा राख्यो, जुन भूमिका पेरिसले पहिले भरेको थियो। यद्यपि "अमूर्त अभिव्यक्तिवाद" भन्ने शव्द पहिलो पटक १ art 66 मा अमेरिकी कलाको लागि कला आलोचक रोबर्ट कोट्सले प्रयोग गरे पनि यो १ 19 १ in मा जर्मन अभिव्यक्तिवाद सम्बन्धी डेर स्टर्म नामक पत्रिकामा जर्मनीमा पहिलो पटक प्रयोग भएको थियो। संयुक्त राज्यमा अल्फ्रेड बार १ 29 २ in मा वासिली कन्डिन्स्कीले गरेको कामको सम्बन्धमा यो शब्द प्रयोग गर्ने पहिलो व्यक्ति थिए।
सार अभिव्यक्तिवाद: अमूर्त अभिव्यक्तिवाद एक पोष्ट हो - अमेरिकी चित्रकलामा दोस्रो विश्व युद्ध कला आन्दोलन, १ 40 .० को दशकमा न्यू योर्कमा विकसित भयो। यो पहिलो विशेष गरी अमेरिकी अभियान हो जसले अन्तर्राष्ट्रिय प्रभाव प्राप्त गर्‍यो र न्यू योर्क शहरलाई पश्चिमी कला विश्वको केन्द्रमा राख्यो, जुन भूमिका पेरिसले पहिले भरेको थियो। यद्यपि "अमूर्त अभिव्यक्तिवाद" भन्ने शव्द पहिलो पटक १ art 66 मा अमेरिकी कलाको लागि कला आलोचक रोबर्ट कोट्सले प्रयोग गरे पनि यो १ 19 १ in मा जर्मन अभिव्यक्तिवाद सम्बन्धी डेर स्टर्म नामक पत्रिकामा जर्मनीमा पहिलो पटक प्रयोग भएको थियो। संयुक्त राज्यमा अल्फ्रेड बार १ 29 २ in मा वासिली कन्डिन्स्कीले गरेको कामको सम्बन्धमा यो शब्द प्रयोग गर्ने पहिलो व्यक्ति थिए।
सार अभिव्यक्तिवाद: अमूर्त अभिव्यक्तिवाद एक पोष्ट हो - अमेरिकी चित्रकलामा दोस्रो विश्व युद्ध कला आन्दोलन, १ 40 .० को दशकमा न्यू योर्कमा विकसित भयो। यो पहिलो विशेष गरी अमेरिकी अभियान हो जसले अन्तर्राष्ट्रिय प्रभाव प्राप्त गर्‍यो र न्यू योर्क शहरलाई पश्चिमी कला विश्वको केन्द्रमा राख्यो, जुन भूमिका पेरिसले पहिले भरेको थियो। यद्यपि "अमूर्त अभिव्यक्तिवाद" भन्ने शव्द पहिलो पटक १ art 66 मा अमेरिकी कलाको लागि कला आलोचक रोबर्ट कोट्सले प्रयोग गरे पनि यो १ 19 १ in मा जर्मन अभिव्यक्तिवाद सम्बन्धी डेर स्टर्म नामक पत्रिकामा जर्मनीमा पहिलो पटक प्रयोग भएको थियो। संयुक्त राज्यमा अल्फ्रेड बार १ 29 २ in मा वासिली कन्डिन्स्कीले गरेको कामको सम्बन्धमा यो शब्द प्रयोग गर्ने पहिलो व्यक्ति थिए।
सार अभिव्यक्तिवाद: अमूर्त अभिव्यक्तिवाद एक पोष्ट हो - अमेरिकी चित्रकलामा दोस्रो विश्व युद्ध कला आन्दोलन, १ 40 .० को दशकमा न्यू योर्कमा विकसित भयो। यो पहिलो विशेष गरी अमेरिकी अभियान हो जसले अन्तर्राष्ट्रिय प्रभाव प्राप्त गर्‍यो र न्यू योर्क शहरलाई पश्चिमी कला विश्वको केन्द्रमा राख्यो, जुन भूमिका पेरिसले पहिले भरेको थियो। यद्यपि "अमूर्त अभिव्यक्तिवाद" भन्ने शव्द पहिलो पटक १ art 66 मा अमेरिकी कलाको लागि कला आलोचक रोबर्ट कोट्सले प्रयोग गरे पनि यो १ 19 १ in मा जर्मन अभिव्यक्तिवाद सम्बन्धी डेर स्टर्म नामक पत्रिकामा जर्मनीमा पहिलो पटक प्रयोग भएको थियो। संयुक्त राज्यमा अल्फ्रेड बार १ 29 २ in मा वासिली कन्डिन्स्कीले गरेको कामको सम्बन्धमा यो शब्द प्रयोग गर्ने पहिलो व्यक्ति थिए।
सार कारखाना ढाँचा: अमूर्त कारखाना बान्कीले व्यक्तिगत कारखानाको समूहलाई समाहित गर्ने तरीका प्रदान गर्दछ जुन तिनीहरूको कंक्रीट वर्ग निर्दिष्ट नगरीकन साझा विषयवस्तु हो। सामान्य प्रयोगमा, क्लाइन्ट सफ्टवेयरले अमूर्त कारखानाको ठोस कार्यान्वयन सिर्जना गर्दछ र त्यसपछि कारखानाको जेनेरिक ईन्टरफेस थ्रीमको अंश भएका ठोस वस्तुहरू सिर्जना गर्न प्रयोग गर्दछ। ग्राहकलाई थाहा छैन कुन यी ठोस वस्तुहरू यी यी प्रत्येक आन्तरिक कारखानाहरूबाट प्राप्त गर्दछन्, किनकि यसले उनीहरूका उत्पादनहरूको सामान्य ईन्टरफेस मात्र प्रयोग गर्दछ। यस बान्कीले वस्तुहरूको सेटको कार्यान्वयनको विवरण तिनीहरूको सामान्य प्रयोगबाट अलग गर्दछ र वस्तु संरचनामा निर्भर गर्दछ, किनभने वस्तु निर्माण कारखाना ईन्टरफेसमा उजागर गरिएका विधिहरूमा लागू हुन्छ।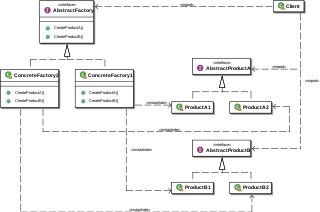
सार कारखाना ढाँचा: अमूर्त कारखाना बान्कीले व्यक्तिगत कारखानाको समूहलाई समाहित गर्ने तरीका प्रदान गर्दछ जुन तिनीहरूको कंक्रीट वर्ग निर्दिष्ट नगरीकन साझा विषयवस्तु हो। सामान्य प्रयोगमा, क्लाइन्ट सफ्टवेयरले अमूर्त कारखानाको ठोस कार्यान्वयन सिर्जना गर्दछ र त्यसपछि कारखानाको जेनेरिक ईन्टरफेस थ्रीमको अंश भएका ठोस वस्तुहरू सिर्जना गर्न प्रयोग गर्दछ। ग्राहकलाई थाहा छैन कुन यी ठोस वस्तुहरू यी यी प्रत्येक आन्तरिक कारखानाहरूबाट प्राप्त गर्दछन्, किनकि यसले उनीहरूका उत्पादनहरूको सामान्य ईन्टरफेस मात्र प्रयोग गर्दछ। यस बान्कीले वस्तुहरूको सेटको कार्यान्वयनको विवरण तिनीहरूको सामान्य प्रयोगबाट अलग गर्दछ र वस्तु संरचनामा निर्भर गर्दछ, किनभने वस्तु निर्माण कारखाना ईन्टरफेसमा उजागर गरिएका विधिहरूमा लागू हुन्छ।
सार कारखाना ढाँचा: अमूर्त कारखाना बान्कीले व्यक्तिगत कारखानाको समूहलाई समाहित गर्ने तरीका प्रदान गर्दछ जुन तिनीहरूको कंक्रीट वर्ग निर्दिष्ट नगरीकन साझा विषयवस्तु हो। सामान्य प्रयोगमा, क्लाइन्ट सफ्टवेयरले अमूर्त कारखानाको ठोस कार्यान्वयन सिर्जना गर्दछ र त्यसपछि कारखानाको जेनेरिक ईन्टरफेस थ्रीमको अंश भएका ठोस वस्तुहरू सिर्जना गर्न प्रयोग गर्दछ। ग्राहकलाई थाहा छैन कुन यी ठोस वस्तुहरू यी यी प्रत्येक आन्तरिक कारखानाहरूबाट प्राप्त गर्दछन्, किनकि यसले उनीहरूका उत्पादनहरूको सामान्य ईन्टरफेस मात्र प्रयोग गर्दछ। यस बान्कीले वस्तुहरूको सेटको कार्यान्वयनको विवरण तिनीहरूको सामान्य प्रयोगबाट अलग गर्दछ र वस्तु संरचनामा निर्भर गर्दछ, किनभने वस्तु निर्माण कारखाना ईन्टरफेसमा उजागर गरिएका विधिहरूमा लागू हुन्छ।
स्वीकारकर्ताहरूको सार परिवार: स्वीकारकर्ताहरूको एक अमूर्त परिवार (एएफए) सामान्यीकृत स्वीकारकर्ताहरूको समूह हो। अनौपचारिक रूपमा, एक स्वीकारकर्ता एक सीमित राज्य नियन्त्रण, एक सीमा संख्या इनपुट प्रतीक, र एक आन्तरिक स्टोर एक पढ्ने र लेख्ने प्रकार्यको साथ एक उपकरण हो। प्रत्येक स्वीकारकर्ताको सुरूवात राज्य र स्वीकार राज्यहरूको सेट हुन्छ। यस उपकरणले प्रतीकहरूको अनुक्रम पढ्दछ, प्रत्येक इनपुट प्रतीकको लागि राज्य देखि राज्यमा परिवर्तन। यदि उपकरण स्वीकार्य स्थितिमा समाप्त हुन्छ भने, उपकरण प्रतीकहरूको अनुक्रम स्वीकार्न भनिन्छ। स्वीकारकर्ताहरूको परिवार एक प्रकारको आन्तरिक स्टोरको साथ स्वीकारकर्ताहरूको सेट हो। AFA को अध्ययन AFL सिद्धान्तको अंश हो।
भाषाहरूको सार परिवार: कम्प्युटर विज्ञानमा, विशेष गरी औपचारिक भाषा सिद्धान्तको क्षेत्रमा, भाषाहरूको एउटा अमूर्त परिवार भनेको नियमित भाषाहरू, प्रसंग-मुक्त भाषाहरू र दोहोरिने असंख्य भाषाहरू, र औपचारिक भाषाहरूका अन्य परिवारहरूका लागि सामान्य विशेषताहरू एक गणितीय धारणा हो। वैज्ञानिक साहित्य मा।
गैर कथा फिल्म: गैर-कथा फिल्म सिनेमाई फिल्मको सौन्दर्य हो जुन वर्णन गर्दैन, वा सम्बन्धित छैन "घटना, वास्तविक वा काल्पनिक"। यो सामान्यतया आर्ट फिल्म वा प्रयोगात्मक फिल्मको एक रूप हो, बड़े मनोरन्जनको लागि बनाइएको छैन।
गैर कथा फिल्म: गैर-कथा फिल्म सिनेमाई फिल्मको सौन्दर्य हो जुन वर्णन गर्दैन, वा सम्बन्धित छैन "घटना, वास्तविक वा काल्पनिक"। यो सामान्यतया आर्ट फिल्म वा प्रयोगात्मक फिल्मको एक रूप हो, बड़े मनोरन्जनको लागि बनाइएको छैन।
सार: अमूर्तले सन्दर्भ गर्न सक्दछ: एब्स्ट्र्याक्ट (एल्बम) , जो ह्यारियट द्वारा १ 62 .२ एल्बम सार (कानून), कानूनी कागजातको सारांश सार (सारांश), शैक्षिक प्रकाशन मा अमूर्त कला, कलात्मक कार्यहरू जुन वास्तविकता वा ठोस विषयहरूको प्रतिनिधित्व गर्ने प्रयास गर्दैन सार: डिजाइन अफ आर्ट , २०१ Net नेटफ्लिक्स दस्तावेजी श्रृंखला अमूर्त संगीत, संगीत जुन गैर-प्रतिनिधित्व हो दर्शनमा अमूर्त वस्तु गणितमा अमूर्त संरचना कम्प्युटर विज्ञानमा अमूर्त प्रकार अमूर्तको सम्पत्ति Q-Tip (संगीतकार), "Abstract" को रूपमा पनि चिनिन्छ
अमूर्त रणनीति खेल: एउटा अमूर्त रणनीति खेल एक रणनीति खेल हो जसमा विषयवस्तु खेल्ने अनुभवको लागि महत्त्वपूर्ण छैन। चेस, गो, चेकर्स र ड्राफ्ट, झ्याiang्गकी, शोगी, रिभर्सी, नौ पुरूष मोरिस, र धेरै म्यानकला भेरियन्ट सहित विश्वका धेरै क्लासिक बोर्ड खेलहरू यस श्रेणीमा फिट छन्, किनकि डेमेओ, हिभ, र YINSH जस्ता अधिक आधुनिक पुनरावृत्तिहरू। ।
सार ग्राफिकल डाटा प्रकार: एउटा अमूर्त ग्राफिकल डाटा प्रकार ( AGDT ) कम्प्यूटर ग्राफिक्सको लागि एब्स्ट्र्याक्ट डाटा प्रकारको एक विस्तार हो। AGDTs ले संरचनात्मक रूपमा ग्राफिकल वस्तुहरू निर्माण गर्न सुविधाहरूको साथ ADT को लाभ प्रदान गर्दछ। औपचारिक रूपमा, AGDT लाई "ग्राफिकल वस्तुहरूको वर्गको रूपमा परिभाषित गर्न सकिन्छ जसको तार्किक व्यवहार ग्राफिकल विशेषताहरूको सेट र ग्राफिकल अपरेशन्सको सेट" द्वारा परिभाषित गरिएको छ।
समूह सिद्धान्त: गणित र अमूर्त बीजगणितमा समूह सिद्धान्तले बीजगणित संरचनाहरूको अध्ययन गर्दछ जसलाई समूह भनिन्छ। समूहको अवधारणा अमूर्त बीजगणितको लागि केन्द्रीय हो: अन्य प्रसिद्ध बीजगणित संरचनाहरू, जस्तै रिंगहरू, क्षेत्रहरू, र भेक्टर स्पेसहरू, सबैलाई थप अपरेशनहरू र अक्षसoms्ख्यकहरूको साथ सम्पन्न समूहको रूपमा देख्न सकिन्छ। समूहहरू गणित भरि पुनरावृत्ति हुन्छन्, र समूह सिद्धान्तका विधिहरूले बीजगणितको धेरै भागहरूलाई प्रभाव पारेका छन्। रैखिक बीजगणित समूहहरू र लाइ समूहहरू समूह सिद्धान्तको दुई शाखा हुन् जुन प्रगति अनुभव गरेका छन् र आफ्नै अधिकारमा विषय क्षेत्र भएका छन्।
Harmonic विश्लेषण: हार्मोनिक विश्लेषण भनेको गणितको एक शाखा हो जुन आधारभूत तरंगहरूको सुपरपोजिसनको रूपमा कार्यहरू वा संकेतहरूको प्रतिनिधित्व, र फ्यूरियर श्रृंखला र फुरियर रूपान्तरणहरूको धारणाको अध्ययन र सामान्यीकरणसँग सम्बन्धित छ। विगत दुई शताब्दीहरूमा, यो संख्या सिद्धान्त, प्रतिनिधित्व सिद्धान्त, संकेत प्रसंस्करण, क्वान्टम मेकानिक्स, ज्वार विश्लेषण र न्यूरो साइंस जस्ता विविध क्षेत्रहरूमा अनुप्रयोगहरूको साथ एक विशाल विषय भएको छ।
वैकल्पिक हिप हप: वैकल्पिक हिप हप हिप हप संगीतको सबजेनर हो जुन मुख्य शैलीको रूपमा पहिचान नभएका शैलीहरूको विस्तृत श्रृंखला समेट्छ। AllMusic ले यसलाई निम्न रूपमा परिभाषित गर्दछ: "वैकल्पिक र्‍यापले हिप हप समूहलाई जनाउँछ जुन र्यापको कुनै पनि परम्परागत स्टीरियोटाइपहरू जस्तै ग्यान्गस्टा, बास, कट्टर, पप, र पार्टी र्यापको अनुरूप इन्कार गर्दछ। यसको सट्टा, तिनीहरू फ्या from्कबाट समान चित्रांकन धमिलो पार्छन्। र पप / रक, साथै जाज, आत्मा, रेगे, र पनि लोक। "
वैकल्पिक हिप हप: वैकल्पिक हिप हप हिप हप संगीतको सबजेनर हो जुन मुख्य शैलीको रूपमा पहिचान नभएका शैलीहरूको विस्तृत श्रृंखला समेट्छ। AllMusic ले यसलाई निम्न रूपमा परिभाषित गर्दछ: "वैकल्पिक र्‍यापले हिप हप समूहलाई जनाउँछ जुन र्यापको कुनै पनि परम्परागत स्टीरियोटाइपहरू जस्तै ग्यान्गस्टा, बास, कट्टर, पप, र पार्टी र्यापको अनुरूप इन्कार गर्दछ। यसको सट्टा, तिनीहरू फ्या from्कबाट समान चित्रांकन धमिलो पार्छन्। र पप / रक, साथै जाज, आत्मा, रेगे, र पनि लोक। "
वैकल्पिक हिप हप: वैकल्पिक हिप हप हिप हप संगीतको सबजेनर हो जुन मुख्य शैलीको रूपमा पहिचान नभएका शैलीहरूको विस्तृत श्रृंखला समेट्छ। AllMusic ले यसलाई निम्न रूपमा परिभाषित गर्दछ: "वैकल्पिक र्‍यापले हिप हप समूहलाई जनाउँछ जुन र्यापको कुनै पनि परम्परागत स्टीरियोटाइपहरू जस्तै ग्यान्गस्टा, बास, कट्टर, पप, र पार्टी र्यापको अनुरूप इन्कार गर्दछ। यसको सट्टा, तिनीहरू फ्या from्कबाट समान चित्रांकन धमिलो पार्छन्। र पप / रक, साथै जाज, आत्मा, रेगे, र पनि लोक। "
Homotopy सिद्धान्त: गणितमा homotopy सिद्धान्त एक परिस्थितिगत व्यवस्थित अध्ययन हो जुन मा नक्शा ती दुवैको बीचमा homotopies संग आउँछ। यो बीजगणित टोपोलजी मा एक शीर्षक को रूप मा उत्पत्ति तर आजकल यो एक स्वतन्त्र अनुशासन को रूप मा अध्ययन गरिएको छ। बीजगणित टोपोलजी बाहेक, सिद्धान्त गणितको अन्य क्षेत्रहरुमा पनि प्रयोग भएको छ जस्तै बीजगणित ज्यामिति (उदाहरणका लागि, A १ homotopy सिद्धान्त ) र कोटि थियरी (विशेष गरी उच्च कोटिहरूको अध्ययन)।
अमूर्त भ्रमवाद: अमूर्त भ्रमवाद , नाम १ 19 67 Barb मा कला इतिहासकार र आलोचक बार्बरा रोज द्वारा बनाईएको। लुइस के। मीसेलले १ ly .० को दशकको बीचमा संयुक्त राज्य अमेरिकामा प्रख्यात भएको कलात्मक आन्दोलनलाई परिभाषित गर्न स्वतन्त्र रूपमा यो शब्दको रचना गरे।
सार कला: अमूर्त कलाले आकार, फार्म, रंग र रेखाको दृश्य भाषा प्रयोग गर्दछ रचना सिर्जना गर्न जुन विश्वमा दृश्य सन्दर्भहरूबाट स्वतन्त्रताको डिग्रीको साथ अवस्थित हुन सक्छ। पश्चिमी कला १ th औं शताब्दीको बीचमा नवजागरणदेखि मध्य परिप्रेक्ष्यमा थियो, परिप्रेक्ष्यको तर्क र दृश्यता वास्तविकताको भ्रम पुनः उत्पन्न गर्ने प्रयासले समेट्यो। १ th औं शताब्दीको अन्तसम्ममा धेरै कलाकारहरूले नयाँ किसिमको कला सिर्जना गर्ने आवश्यकता महसुस गरे जुन टेक्नोलोजी, विज्ञान र दर्शनमा हुने मौलिक परिवर्तनहरूलाई समेट्ने थियो। स्रोतबाट व्यक्ति कलाकारहरूले उनीहरूको सैद्धांतिक तर्कहरू विविध थिए, र त्यो समयको पश्चिमी संस्कृतिको सबै क्षेत्रमा सामाजिक र बौद्धिक व्याकुलता प्रतिबिम्बित गर्दछ।
सार छविहरू: एब्स्ट्र्याक्ट इमेजिस्टहरू एक शब्द हो जुन १। .१ सालको गुग्नेहेम संग्रहालय, न्यू योर्कमा अमेरिकी एब्स्ट्र्याक्ट एक्सप्रेशनिस्ट्स र इमेजिस्ट भनिन्छ। अमेरिकी र युरोपेली चित्रकला र मूर्तिकलाको प्रवृत्तिको अनुसन्धानका लागि कार्यक्रमहरूको श्रृंखलामा यो प्रदर्शनी पहिलो थियो।
सार छविहरू: एब्स्ट्र्याक्ट इमेजिस्टहरू एक शब्द हो जुन १। .१ सालको गुग्नेहेम संग्रहालय, न्यू योर्कमा अमेरिकी एब्स्ट्र्याक्ट एक्सप्रेशनिस्ट्स र इमेजिस्ट भनिन्छ। अमेरिकी र युरोपेली चित्रकला र मूर्तिकलाको प्रवृत्तिको अनुसन्धानका लागि कार्यक्रमहरूको श्रृंखलामा यो प्रदर्शनी पहिलो थियो।
अमूर्त छाप: एब्स्ट्र्याक्ट इम्प्रेशनवाद एक कला आन्दोलन हो जुन १ New s० को दशकमा न्यू योर्क शहरमा शुरू भयो। यसले ईम्प्रेशनिस्ट-शैलीमा वास्तविक-जीवन दृश्यहरू, वस्तुहरू वा व्यक्ति (चित्र) जस्ता विषयको चित्रकला समावेश गर्दछ, तर अमूर्तिको विभिन्न उपायहरूमा जोड दिइन्छ। चित्रहरू प्राय: एन प्लीइन एअरमा चित्रित हुन्छन् , एक कलात्मक शैली जसमा चित्रकार समावेश हुन्छ बाहेक चित्रकलाको सीधा कलाकारको अगाडि। आन्दोलन शुद्ध अमूर्त रेखा र चित्रकलामा वास्तविकता को एक छाप को भत्ता को बीच नाजुक काम गर्दछ।
अमूर्त छाप: एब्स्ट्र्याक्ट इम्प्रेशनवाद एक कला आन्दोलन हो जुन १ New s० को दशकमा न्यू योर्क शहरमा शुरू भयो। यसले ईम्प्रेशनिस्ट-शैलीमा वास्तविक-जीवन दृश्यहरू, वस्तुहरू वा व्यक्ति (चित्र) जस्ता विषयको चित्रकला समावेश गर्दछ, तर अमूर्तिको विभिन्न उपायहरूमा जोड दिइन्छ। चित्रहरू प्राय: एन प्लीइन एअरमा चित्रित हुन्छन् , एक कलात्मक शैली जसमा चित्रकार समावेश हुन्छ बाहेक चित्रकलाको सीधा कलाकारको अगाडि। आन्दोलन शुद्ध अमूर्त रेखा र चित्रकलामा वास्तविकता को एक छाप को भत्ता को बीच नाजुक काम गर्दछ।
सार सूचकांक अंकन: एब्स्ट्र्याक्ट इन्डेक्स नोटेशन टेन्सर र स्पिनरहरूको लागि गणितीय अंकन हो जुन सूचकांकहरू तिनीहरूको प्रकारहरू संकेत गर्न प्रयोग गर्दछ, एक विशेष आधारमा तिनीहरूको कम्पोनेन्टहरू भन्दा। सूचकांक केवल प्लेसहोल्डरहरू हुन्, कुनै आधारसँग सम्बन्धित हुँदैन र, विशेष रूपमा गैर-संख्यात्मक हो। यसैले यसलाई रिक्सी क्यालकुलस संग भ्रमित गर्नु हुँदैन। आइटरन सम्मेलन सम्मेलनका औपचारिक पक्षहरूलाई आधुनिक अमूर्त टेन्सर संकेतनमा संकुचन र कोभेरियन्ट भेदभाव वर्णन गर्नमा कठिनाईलाई क्षतिपूर्ति दिनको लागि यो परिचयपत्र परिचयको रूपमा प्रस्तुत गरिएको थियो, जबकि त्यसमा समावेश भएका अभिव्यक्तिहरूको स्पष्ट संगमलाई जोगाउँदै।
अनुक्रमणिका समूह: अपरेटर सिद्धान्तमा, गणितको शाखा, प्रत्येक बनच बीजगणित एउटा समूहसँग सम्बन्धित हुन सक्छ जुन यसको एब्स्ट्र्याक्ट इन्डेक्स समूह भनिन्छ ।
सार सूचकांक अंकन: एब्स्ट्र्याक्ट इन्डेक्स नोटेशन टेन्सर र स्पिनरहरूको लागि गणितीय अंकन हो जुन सूचकांकहरू तिनीहरूको प्रकारहरू संकेत गर्न प्रयोग गर्दछ, एक विशेष आधारमा तिनीहरूको कम्पोनेन्टहरू भन्दा। सूचकांक केवल प्लेसहोल्डरहरू हुन्, कुनै आधारसँग सम्बन्धित हुँदैन र, विशेष रूपमा गैर-संख्यात्मक हो। यसैले यसलाई रिक्सी क्यालकुलस संग भ्रमित गर्नु हुँदैन। आइटरन सम्मेलन सम्मेलनका औपचारिक पक्षहरूलाई आधुनिक अमूर्त टेन्सर संकेतनमा संकुचन र कोभेरियन्ट भेदभाव वर्णन गर्नमा कठिनाईलाई क्षतिपूर्ति दिनको लागि यो परिचयपत्र परिचयको रूपमा प्रस्तुत गरिएको थियो, जबकि त्यसमा समावेश भएका अभिव्यक्तिहरूको स्पष्ट संगमलाई जोगाउँदै।
सार सूचकांक अंकन: एब्स्ट्र्याक्ट इन्डेक्स नोटेशन टेन्सर र स्पिनरहरूको लागि गणितीय अंकन हो जुन सूचकांकहरू तिनीहरूको प्रकारहरू संकेत गर्न प्रयोग गर्दछ, एक विशेष आधारमा तिनीहरूको कम्पोनेन्टहरू भन्दा। सूचकांक केवल प्लेसहोल्डरहरू हुन्, कुनै आधारसँग सम्बन्धित हुँदैन र, विशेष रूपमा गैर-संख्यात्मक हो। यसैले यसलाई रिक्सी क्यालकुलस संग भ्रमित गर्नु हुँदैन। आइटरन सम्मेलन सम्मेलनका औपचारिक पक्षहरूलाई आधुनिक अमूर्त टेन्सर संकेतनमा संकुचन र कोभेरियन्ट भेदभाव वर्णन गर्नमा कठिनाईलाई क्षतिपूर्ति दिनको लागि यो परिचयपत्र परिचयको रूपमा प्रस्तुत गरिएको थियो, जबकि त्यसमा समावेश भएका अभिव्यक्तिहरूको स्पष्ट संगमलाई जोगाउँदै।
बौद्धिक एजेन्ट: कृत्रिम बुद्धिमत्तामा, एक बुद्धिमान एजेन्ट ( आईए ) ले एक स्वायत्त संस्थालाई जनाउँछ जसले काम गर्दछ, लक्षहरू प्राप्त गर्नेतर्फ आफ्नो गतिविधि निर्देशित गर्दछ, वातावरणमा सेन्सरहरू र त्यसको परिणामस्वरूप एक्ट्युएटरहरू मार्फत अवलोकन प्रयोग गरेर। बौद्धिक एजेन्टहरूले पनि ज्ञान प्राप्त गर्न वा आफ्ना लक्ष्यहरू प्राप्त गर्न प्रयोग गर्न सक्दछन्। तिनीहरू धेरै सरल वा धेरै जटिल हुन सक्छन्। एक रिफ्लेक्स मेशीन, जस्तै एक थर्मोस्टेट, एक बुद्धिमान एजेन्ट को एक उदाहरण को रूप मा मानिन्छ।
अमूर्त तह: कम्प्युटि Inमा एउटा एब्स्ट्रक्शन लेयर वा अमूर्त स्तर भनेको उपप्रणालीको कामका विवरणहरू लुकाउने एउटा तरिका हो, चिन्ताको अलगकरणलाई अन्तर्क्रियात्मकता र प्लेटफर्म स्वतन्त्रताको सुविधाका लागि। सफ्टवेयर मोडेलको उदाहरणहरूले एब्स्ट्र्यासनको लेयरहरू प्रयोग गर्छन् नेटवर्क प्रोटोकल, ओपनजीएल र अन्य ग्राफिक्स लाइब्रेरीहरूको लागि ओएसआई मोडेल।
अमूर्त व्याख्या: कम्प्युटर विज्ञानमा, अमूर्त व्याख्या भनेको कम्प्युटर प्रोग्रामहरूको शान्तिकरणको ध्वनि सx्केतको सिद्धान्त हो, मोन्डोटोनिक प्रकार्यहरूमा आधारित अर्डर गरिएका सेटहरू, विशेष गरी ल्याटिसहरूको आधारमा। यो एक कम्प्युटर प्रोग्रामको आंशिक कार्यान्वयनको रूपमा देख्न सकिन्छ जुन सबै गणनाहरू बिना यसको अर्थको बारेमा जानकारी प्राप्त गर्दछ।
अमूर्त व्याख्या: कम्प्युटर विज्ञानमा, अमूर्त व्याख्या भनेको कम्प्युटर प्रोग्रामहरूको शान्तिकरणको ध्वनि सx्केतको सिद्धान्त हो, मोन्डोटोनिक प्रकार्यहरूमा आधारित अर्डर गरिएका सेटहरू, विशेष गरी ल्याटिसहरूको आधारमा। यो एक कम्प्युटर प्रोग्रामको आंशिक कार्यान्वयनको रूपमा देख्न सकिन्छ जुन सबै गणनाहरू बिना यसको अर्थको बारेमा जानकारी प्राप्त गर्दछ।
सार श्रम र ठोस श्रम: अमूर्त श्रम र ठोस श्रमले राजनीतिक अर्थव्यवस्थाको उनको आलोचनामा कार्ल मार्क्सले गरेको भिन्नतालाई जनाउँछ। यो एक विशेष उपयोगी प्रभाव छ कि एक विशेष गतिविधि को रूप मा मानव श्रम आर्थिक रूप मा मूल्यवान कार्य समय को रूप मा सामान्य रूप मा मानव श्रम बीचको भिन्नता लाई दर्शाउँछ।
सार श्रम र ठोस श्रम: अमूर्त श्रम र ठोस श्रमले राजनीतिक अर्थव्यवस्थाको उनको आलोचनामा कार्ल मार्क्सले गरेको भिन्नतालाई जनाउँछ। यो एक विशेष उपयोगी प्रभाव छ कि एक विशेष गतिविधि को रूप मा मानव श्रम आर्थिक रूप मा मूल्यवान कार्य समय को रूप मा सामान्य रूप मा मानव श्रम बीचको भिन्नता लाई दर्शाउँछ।
सार श्रम र ठोस श्रम: अमूर्त श्रम र ठोस श्रमले राजनीतिक अर्थव्यवस्थाको उनको आलोचनामा कार्ल मार्क्सले गरेको भिन्नतालाई जनाउँछ। यो एक विशेष उपयोगी प्रभाव छ कि एक विशेष गतिविधि को रूप मा मानव श्रम आर्थिक रूप मा मूल्यवान कार्य समय को रूप मा सामान्य रूप मा मानव श्रम बीचको भिन्नता लाई दर्शाउँछ।
अमूर्त तर्क: गणितीय तर्कमा, एउटा अमूर्त तर्क भनेको औपचारिक प्रणाली हो जसमा वाक्यको वर्ग हुन्छ र घटना, विस्तार, आइसोमोर्फिज्म, पुन: नामाकरण र परिमाणिकरण सम्बन्धी विशिष्ट गुणहरूसँग सन्तुष्टि सम्बन्ध हुन्छ।
सार तर्क (असंतोष): एब्स्ट्र्याक्ट तर्क एक औपचारिक प्रणाली हो जुन वाक्यको वर्ग हुन्छ र विशिष्ट सम्पत्तीसँग सन्तुष्टि सम्बन्ध हुन्छ।
एब्स्ट्र्याक्ट एम-स्पेस: गणितमा, विशेष रूपमा अर्डर सिद्धान्त र कार्यात्मक विश्लेषणमा, एउटा अमूर्त m -space वा AM- Space भनेको एक Banach जाली हो जसको आदर्श सन्तुष्ट हुन्छ सबै x र y को लागी X को धनात्मक शंकुमा। हामी त्यहाँ बाहेक केही यू ≥ 0 मा एक्स यस्तो अवस्थित छ भने एक AM-स्पेस एक्स एकाइ एउटा AM-ठाउँ छ भनेर भन्न कि अन्तराल [- यू, यू]: = {Z ∈ एक्स: - यू ≤ Z र Z ≤ u X X को एकाइ बल बराबर हो; यस्तो एलिमेन्ट यू अद्वितीय र X को अर्डर एकाइ हो।
सार मेशिन: एउटा एब्स्ट्र्याक्ट मेशिन , जसलाई एब्स्ट्र्याक्ट कम्प्यूटर पनि भनिन्छ, एक सैद्धांतिक कम्प्युटर हो जुन गणनाको मोडेल परिभाषित गर्न प्रयोग गरिन्छ। कम्प्युटि processes प्रक्रियाहरूको एब्स्ट्र्यासन दुबै कम्प्युटर विज्ञान र कम्प्युटर ईन्जिनियरि discip विषयहरूमा प्रयोग गरिन्छ र सामान्यतया एक असक्रिय समय प्रतिमान ग्रहण गर्दछ।
B- विधि: बी विधि सफ्टवेयर विकासको बीमा आधारित एक विधि हो, कम्प्यूटर सफ्टवेयरको विकासमा प्रयोग गरिएको एब्स्ट्र्याक्ट मेशिन नोटसनमा आधारित एक उपकरण समर्थित औपचारिक विधि। यो १ 1980 France० को दशकमा फ्रान्स र बेलायतको जीन रेमंड एब्रियलले विकसित गरेको हो। बी Z संकेतसँग सम्बन्धित छ र विशिष्टीकरणहरूबाट प्रोग्रामिंग भाषा कोडको विकासलाई समर्थन गर्दछ। बी यूरोपमा प्रमुख सुरक्षा-महत्वपूर्ण प्रणाली अनुप्रयोगहरूमा प्रयोग भएको छ। यो विशिष्ट, डिजाइन, प्रूफ र कोड उत्पादनको लागि मजबूत, व्यावसायिक रूपमा उपलब्ध उपकरण समर्थन छ।
सार व्यवस्थापन: एब्स्ट्र्याक्ट प्रबन्धन एक शैक्षिक सम्मेलन मा प्रस्तुतीकरणका लागि एब्स्ट्रक्ट स्वीकार्न र तयार गर्ने प्रक्रिया हो। प्रक्रिया या त आमन्त्रित वा काम को सार सारांश वा सारांश बुझेको हुन्छ। अमूर्तले सामान्यतया परिकल्पना, अनुसन्धान वा अन्वेषणमा प्रयोग गरिएको उपकरणहरू, डेटा संकलित गर्दछ, र डाटाको सारांश वा व्याख्या गर्दछ।
मनिफोल्ड: गणितमा, एक मानिफोल्ड एक टोपोलॉजिकल स्पेस हो जुन स्थानीय रूपमा प्रत्येक बिन्दुको नजिक युक्लिडियन अन्तर मिल्दोजुल्दो छ। थप ठीक, छोटो लागि N -dimensional धेरै गुना, वा N -manifold, प्रत्येक बिन्दु आयाम n को Euclidean ठाउँ गर्न homeomorphic छ कि एक छिमेकी भएको सम्पत्ति एक topological ठाउँ छ।
शुद्ध गणित: शुद्ध गणित गणितको बाहिरी कुनै पनि अनुप्रयोगको स्वतन्त्र रूपमा गणितीय अवधारणाको अध्ययन हो। यी अवधारणाहरू वास्तविक-विश्व चिन्ताहरूमा उत्पन्न हुन सक्छ, र प्राप्त परिणामहरू पछि व्यावहारिक अनुप्रयोगहरूको लागि उपयोगी हुन सक्छ, तर शुद्ध गणितज्ञहरू त्यस्ता अनुप्रयोगहरू द्वारा प्राथमिक रूपमा प्रेरित छैनन्। यसको सट्टा, अपीललाई आधारभूत सिद्धान्तहरूको तार्किक परिणामहरू कार्य गर्ने बौद्धिक चुनौती र सौन्दर्य सौन्दर्यलाई जिम्मेवार छ।
गणितीय वस्तु: गणितिय वस्तु भनेको गणितमा उत्पन्न हुने एउटा अमूर्त अवधारणा हो। गणितको सामान्य भाषामा कुनै पनि वस्तु औपचारिक रूपमा परिभाषित गरिएको हुन्छ र जसको साथले घटाउने तर्क र गणितको प्रमाण गर्न सकिन्छ। सामान्यतया, एक गणितीय वस्तु एक मान हुन सक्दछ जुन एउटा भ्यारीएबलमा तोकिन्छ, र त्यसैले सूत्रहरुमा सामेल हुन सक्छ। सामान्य रूपमा सामना गरिएको गणितिय वस्तुहरूले नम्बरहरू, सेटहरू, प्रकार्यहरू, अभिव्यक्तिहरू, ज्यामितीय आकारहरू, अन्य गणितीय वस्तुहरूको रूपान्तरण, र खाली ठाउँहरू समावेश गर्दछ। गणितीय वस्तुहरू धेरै जटिल हुन सक्छन्; उदाहरण को लागी, प्रमेय, प्रमाणहरु, र सिद्धान्तहरु पनि प्रमाण सिद्धान्त मा गणितीय वस्तुहरु को रूप मा मानिन्छ।
गणितीय समस्या: गणितिय समस्या भनेको एक समस्या हो जुन गणितको विधिहरू मार्फत प्रतिनिधित्व गर्ने, विश्लेषण गर्ने र सम्भव हुने समाधानको लागि योग्य छ। यो वास्तविक विश्व समस्या हुन सक्छ, जस्तै सौर प्रणालीमा ग्रहहरूको कक्षा गणना, वा अधिक अमूर्त प्रकृति को समस्या, जस्तै हिल्बर्टको समस्या। यो पनि गणितको प्रकृतिलाई संदर्भित गर्न समस्या हुन सक्छ, जस्तै रसेलको प्याराडक्स।
शुद्ध गणित: शुद्ध गणित गणितको बाहिरी कुनै पनि अनुप्रयोगको स्वतन्त्र रूपमा गणितीय अवधारणाको अध्ययन हो। यी अवधारणाहरू वास्तविक-विश्व चिन्ताहरूमा उत्पन्न हुन सक्छ, र प्राप्त परिणामहरू पछि व्यावहारिक अनुप्रयोगहरूको लागि उपयोगी हुन सक्छ, तर शुद्ध गणितज्ञहरू त्यस्ता अनुप्रयोगहरू द्वारा प्राथमिक रूपमा प्रेरित छैनन्। यसको सट्टा, अपीललाई आधारभूत सिद्धान्तहरूको तार्किक परिणामहरू कार्य गर्ने बौद्धिक चुनौती र सौन्दर्य सौन्दर्यलाई जिम्मेवार छ।
विधि (कम्प्युटर प्रोग्रामिंग): वस्तु उन्मुख प्रोग्रामिंगमा एक विधि (OOP) प्रक्रिया र सन्देशसँग सम्बन्धित वस्तु हो। एउटा वस्तुमा डाटा र व्यवहार हुन्छन् ; यीले इन्टरफेस समावेश गर्दछ , जसले निर्दिष्ट गर्दछ कि वस्तु कसरी यसको विभिन्न उपभोक्ताहरू मध्ये कुनै एक द्वारा प्रयोग गर्न सकिन्छ।
वैचारिक मोडेल: एक अवधारणागत मोडल प्रणालीको प्रतिनिधित्व हो, अवधारणाको संरचनाबाट बनेको हुन्छ जुन मानिसहरूलाई जान्न, बुझ्न, वा मोडलले प्रतिनिधित्व गर्ने विषय अनुकरण गर्न मद्दतको लागि प्रयोग गरिन्छ। यो अवधारणाहरूको पनि सेट हो। यसको विपरित, भौतिक मोडेलहरू भौतिक वस्तुहरू हुन्; उदाहरण को लागी, एक खेलौना मोडेल जो भेला हुन सक्छ, र यो प्रतिनिधित्व वस्तु जस्तै काम गर्न बनाइन्छ।
अमूर्त मोडल सिद्धान्त: गणितीय तर्कमा, अमूर्त मोडल सिद्धान्त मोडल सिद्धान्तको सामान्यीकरण हो जुन पहिलो अर्डर तर्कको विस्तार र उनीहरूको मोडेलहरूको सामान्य गुणहरूको अध्ययन गर्दछ।
निरपेक्ष संगीत: निरपेक्ष संगीत भनेको संगीत हो जुन स्पष्ट रूपमा "केहि" केहि छैन; कार्यक्रम संगीतको विपरित, यो गैर-प्रतिनिधित्व हो। १ absolute औं शताब्दीको अन्त्यमा विल्हेल्म हेनरिक वाकेनरोडर, लुडविग टेक र ईटीए होफम्यान जस्ता प्रारम्भिक जर्मन रोमान्टिकवादका लेखकहरूको लेखनमा पूर्ण संगीतको विचारको विकास भयो तर यो शब्द १ 184646 सम्ममा बनिएको थिएन जहाँ यो पहिलो पटक रिचर्ड वाग्नरले प्रयोग गरे। बीथोभनको नवौं सिम्फनीको कार्यक्रममा।
अमूर्त बकवास: गणितमा, अमूर्त बकवास , सामान्य अमूर्त बकवास , सामान्यीकृत अमूर्त बकवास , र सामान्य बकवास शब्दहरू गणितज्ञहरूले कोटी सिद्धान्त र होम्योजिकल बीजगणित सम्बन्धित अमूर्त विधिहरू वर्णन गर्न प्रयोग गर्दछन्। सामान्यतया, "अमूर्त बकवास" ले एक प्रमाणलाई बुझाउँदछ जुन श्रेणी-सिद्धान्त विधिहरूमा निर्भर गर्दछ, वा आफ्नै कोटी सिद्धान्तको अध्ययनमा पनि।
संज्ञा: संज्ञा भन्ने शब्द हो जुन कुनै खास वस्तु वा वस्तुहरूको सेटको नामको रूपमा कार्य गर्दछ, जस्तै जीवित प्राणीहरू, ठाउँहरू, कार्यहरू, गुणहरू, अस्तित्वको अवस्था, वा विचारहरू। यद्यपि संज्ञा अर्थपूर्ण श्रेणी होईन, त्यसैले यसको अर्थको हिसाबले यो विशेषता हुन सक्दैन। तसर्थ, कार्यहरू र अस्तित्वको अवस्थाहरू पनि क्रियापदहरू, विशेषणहरूद्वारा गुणहरू, र ठाउँवाचकितहरूद्वारा व्यक्त गर्न सकिन्छ। भाषिक हिसाबले, संज्ञा एक ठूलो, खुला भागको सदस्य हो जसका सदस्यहरू मुख्य शब्दको रूपमा उपधारा, क्रियाको वस्तु, वा पूर्वसूचनाको वस्तुको रूपमा हुन सक्छन्।
कंक्रीट नम्बर: कंक्रीट संख्या वा संख्यात्मक संख्याहरू गणना गरिएको चीजहरूसँग सम्बन्धित संख्या हो जुन एक अमूर्त संख्या वा संख्यात्मक संख्याको विपरित हो जुन एकल एकाइको रूपमा संख्या हो। उदाहरणको लागि, "पाँच स्याउ" र "पाईको आधा" क concrete्क्रीट संख्या हुन्, जबकि "पाँच" र "एक आधा" अमूर्त संख्याहरू हुन्। गणितमा "नम्बर" भन्ने शब्द सामान्यतया अमूर्त संख्याको अर्थ लिइन्छ। डिनोमिनेट नम्बर एक प्रकारको क concrete ्क्रिट संख्या हो जुन यससँग जोडिएको मापनको एकाईसँग छ। उदाहरण को लागी, "inches इन्च" एक डिनोमिनेट नम्बर हो किनकि यसको पछाडि इकाई इन्च हुन्छ ।
कंक्रीट नम्बर: कंक्रीट संख्या वा संख्यात्मक संख्याहरू गणना गरिएको चीजहरूसँग सम्बन्धित संख्या हो जुन एक अमूर्त संख्या वा संख्यात्मक संख्याको विपरित हो जुन एकल एकाइको रूपमा संख्या हो। उदाहरणको लागि, "पाँच स्याउ" र "पाईको आधा" क concrete्क्रीट संख्या हुन्, जबकि "पाँच" र "एक आधा" अमूर्त संख्याहरू हुन्। गणितमा "नम्बर" भन्ने शब्द सामान्यतया अमूर्त संख्याको अर्थ लिइन्छ। डिनोमिनेट नम्बर एक प्रकारको क concrete ्क्रिट संख्या हो जुन यससँग जोडिएको मापनको एकाईसँग छ। उदाहरण को लागी, "inches इन्च" एक डिनोमिनेट नम्बर हो किनकि यसको पछाडि इकाई इन्च हुन्छ ।
सार र ठोस: मेटाफिजिक्समा अमूर्त र कंक्रीट बीचको भिन्नता दुई प्रकारका निकायहरू बीचको विभाजनलाई जनाउँछ। धेरै दार्शनिकहरू भन्छन कि यो भिन्नताको मौलिक मेटाफिजिकल महत्त्व छ। कंक्रीट वस्तुहरूका उदाहरणहरूमा बोटबिरुवा, मानव र ग्रहहरू समावेश छन् जबकि चीजहरू संख्या, सेट र प्रस्तावहरू अमूर्त वस्तुहरू हुन् । संक्षिप्तता र अमूर्तताको चरित्रको चिह्न के हो भन्ने बारे कुनै सहमति छैन। लोकप्रिय सुझावहरूले अन्तरिक्षको बीचमा अन्तर छुट्याउने समावेश गर्दछ (१) अन्तरिक्ष समय भित्र वा बाहिर अवस्थित, (२) कारण र प्रभावहरू हुनु वा नहुनु, ()) आकस्मिक वा आवश्यक अस्तित्व हुनु, ()) विशेष वा विश्वव्यापी हुनु र ()) या त शारीरिक वा मानसिक क्षेत्र बाट सम्बन्धित छ। दृष्टिकोणको यस विविधताको बावजुद, प्रायः वस्तुहरूको बारेमा विस्तृत सम्झौता छ कि तिनीहरू अमूर्त वा क concreteक्रीट हुन्। त्यसोभए प्रायः व्याख्याहरूको अन्तर्गत, यी सबै विचारहरू सहमत हुनेछन्, उदाहरणका लागि, बोटहरू ठोस वस्तुहरू हुन् जबकि संख्याहरू अमूर्त वस्तुहरू हुन्छन्।
अमूर्त वस्तु सिद्धान्त: अमूर्त वस्तु सिद्धान्त ( AOT ) अमूर्त वस्तुहरूको सन्दर्भमा मेटाफिजिक्सको एक शाखा हो। मूलरुपमा १ 198 in१ मा मेटाफिजिक्स एडवर्ड जाल्टा द्वारा बनाएको यो सिद्धान्त गणितीय प्लेटोनिज्मको विस्तार हो।
सार र ठोस: मेटाफिजिक्समा अमूर्त र कंक्रीट बीचको भिन्नता दुई प्रकारका निकायहरू बीचको विभाजनलाई जनाउँछ। धेरै दार्शनिकहरू भन्छन कि यो भिन्नताको मौलिक मेटाफिजिकल महत्त्व छ। कंक्रीट वस्तुहरूका उदाहरणहरूमा बोटबिरुवा, मानव र ग्रहहरू समावेश छन् जबकि चीजहरू संख्या, सेट र प्रस्तावहरू अमूर्त वस्तुहरू हुन् । संक्षिप्तता र अमूर्तताको चरित्रको चिह्न के हो भन्ने बारे कुनै सहमति छैन। लोकप्रिय सुझावहरूले अन्तरिक्षको बीचमा अन्तर छुट्याउने समावेश गर्दछ (१) अन्तरिक्ष समय भित्र वा बाहिर अवस्थित, (२) कारण र प्रभावहरू हुनु वा नहुनु, ()) आकस्मिक वा आवश्यक अस्तित्व हुनु, ()) विशेष वा विश्वव्यापी हुनु र ()) या त शारीरिक वा मानसिक क्षेत्र बाट सम्बन्धित छ। दृष्टिकोणको यस विविधताको बावजुद, प्रायः वस्तुहरूको बारेमा विस्तृत सम्झौता छ कि तिनीहरू अमूर्त वा क concreteक्रीट हुन्। त्यसोभए प्रायः व्याख्याहरूको अन्तर्गत, यी सबै विचारहरू सहमत हुनेछन्, उदाहरणका लागि, बोटहरू ठोस वस्तुहरू हुन् जबकि संख्याहरू अमूर्त वस्तुहरू हुन्छन्।
सम्पत्ति अमूर्त: सम्पत्ति अमूर्त कानूनी कागजातहरूको स is्ग्रह हो जुन भूमिको विशेष पार्सलसँग सम्बन्धित क्रॉनिकल लेनदेन। सामान्यतया: कार्यहरू, धितोहरू, विलहरू, प्रोबेट रेकर्डहरू, अदालत मुद्दा दायरहरू, र कर बिक्री sales मूलतः सम्पत्तिलाई असर गर्ने कुनै पनि कानुनी कागजातको सन्दर्भ हो।
न्यायको सार: " फैसलाको सार " भनेको एक फैसलाको लिखित सार हो जुन बताउँछ कि हराएको प्रतिवादीले मुद्दा जितेको व्यक्तिलाई कति पैसा तिर्नु पर्दछ, न्यायको रकममा ब्याज दर, अदालतको लागत, र कुनै विशेष आदेशहरू कि प्रतिवादी गुमाउनुपर्दा आज्ञापालन गर्नुपर्दछ, जुन अमूर्त मानिन्छ र मोहर लगाईन्छ ताकि यसलाई रेकर्ड गर्न सकिन्छ र सरकारसँग आधिकारिक बनाउँदछ। न्यायको अमूर्तको उद्देश्य भनेको सार्वजनिक रेकर्ड बनाउनु र काउन्टीमा अवस्थित प्रतिवादी द्वारा अधिग्रहण गरिएको कुनै पनि घर जग्गा सम्पत्तिमा आवश्यक परेमा आवश्यक परेमा कानूनी हकवाला वा दावी सिर्जना गर्नु भनेको न्यायको अमूर्त अभिलेख राखिएको छ। यदि हार्ने व्यक्तिले निर्णय स्वेच्छाले भुक्तान गरेन भने विजयीले शेरिफको कुनै पनि सम्पत्ति बेच्न जबरजस्ती गर्न सकीन्छ। त्यहाँ धेरै समस्याहरू छन्: १) काउन्टी पत्ता लगाउन जहाँ हारेको अचल सम्पत्तीको स्वामित्व हुन्छ; २) सुरक्षित loansण, कर दायित्व र / वा अन्य निर्णयहरू छन् जुन निर्णय लिनेको अगाडि आउँछन्; )) सम्भव छ कि हारे / torणी दिवालिया हुन सक्छ र payingण तिर्नबाट बच्न सक्छ।
सम्पत्ति अमूर्त: सम्पत्ति अमूर्त कानूनी कागजातहरूको स is्ग्रह हो जुन भूमिको विशेष पार्सलसँग सम्बन्धित क्रॉनिकल लेनदेन। सामान्यतया: कार्यहरू, धितोहरू, विलहरू, प्रोबेट रेकर्डहरू, अदालत मुद्दा दायरहरू, र कर बिक्री sales मूलतः सम्पत्तिलाई असर गर्ने कुनै पनि कानुनी कागजातको सन्दर्भ हो।
सम्पत्ति अमूर्त: सम्पत्ति अमूर्त कानूनी कागजातहरूको स is्ग्रह हो जुन भूमिको विशेष पार्सलसँग सम्बन्धित क्रॉनिकल लेनदेन। सामान्यतया: कार्यहरू, धितोहरू, विलहरू, प्रोबेट रेकर्डहरू, अदालत मुद्दा दायरहरू, र कर बिक्री sales मूलतः सम्पत्तिलाई असर गर्ने कुनै पनि कानुनी कागजातको सन्दर्भ हो।
केसिनिया (पत्रिका): क्यासिनिया डेलावेयर भ्याली अर्निथोलॉजिकल क्लब (डीभीओसी) को पत्रिका हो। पत्रिका पूर्वी पेन्सल्भेनिया, न्यु जर्सी, र डेलावेयरको पक्षपाती सम्बन्धी कागजातहरू मिलेर बनेको छ। आजसम्म सत्तरी अंकहरू प्रकाशित भएका छन्। Initial आरम्भिक खण्डहरू (१ 18 – -१ 00 ०00) एब्स्ट्रैक्ट अफ प्रोसिसिings ्ग्स अफ डेलावेयर भ्याली अर्निथोलॉजिकल क्लबको नामबाट प्रकाशित भयो, र १ 190 ०१ मा पक्षी विज्ञानी जोन क्यासिनको सम्मानमा उक्त पत्रिकाको नाम परिवर्तन गरियो।
सार (कानून): कानून मा, एक सार एक संक्षिप्त बयान हो कि एक लामो कानूनी कागजात को सबै भन्दा महत्वपूर्ण बिन्दु वा धेरै सम्बन्धित कानूनी कागजात को समावेश गर्दछ।
सम्पत्ति अमूर्त: सम्पत्ति अमूर्त कानूनी कागजातहरूको स is्ग्रह हो जुन भूमिको विशेष पार्सलसँग सम्बन्धित क्रॉनिकल लेनदेन। सामान्यतया: कार्यहरू, धितोहरू, विलहरू, प्रोबेट रेकर्डहरू, अदालत मुद्दा दायरहरू, र कर बिक्री sales मूलतः सम्पत्तिलाई असर गर्ने कुनै पनि कानुनी कागजातको सन्दर्भ हो।
सार कला: अमूर्त कलाले आकार, फार्म, रंग र रेखाको दृश्य भाषा प्रयोग गर्दछ रचना सिर्जना गर्न जुन विश्वमा दृश्य सन्दर्भहरूबाट स्वतन्त्रताको डिग्रीको साथ अवस्थित हुन सक्छ। पश्चिमी कला १ th औं शताब्दीको बीचमा नवजागरणदेखि मध्य परिप्रेक्ष्यमा थियो, परिप्रेक्ष्यको तर्क र दृश्यता वास्तविकताको भ्रम पुनः उत्पन्न गर्ने प्रयासले समेट्यो। १ th औं शताब्दीको अन्तसम्ममा धेरै कलाकारहरूले नयाँ किसिमको कला सिर्जना गर्ने आवश्यकता महसुस गरे जुन टेक्नोलोजी, विज्ञान र दर्शनमा हुने मौलिक परिवर्तनहरूलाई समेट्ने थियो। स्रोतबाट व्यक्ति कलाकारहरूले उनीहरूको सैद्धांतिक तर्कहरू विविध थिए, र त्यो समयको पश्चिमी संस्कृतिको सबै क्षेत्रमा सामाजिक र बौद्धिक व्याकुलता प्रतिबिम्बित गर्दछ।
सार कला: अमूर्त कलाले आकार, फार्म, रंग र रेखाको दृश्य भाषा प्रयोग गर्दछ रचना सिर्जना गर्न जुन विश्वमा दृश्य सन्दर्भहरूबाट स्वतन्त्रताको डिग्रीको साथ अवस्थित हुन सक्छ। पश्चिमी कला १ th औं शताब्दीको बीचमा नवजागरणदेखि मध्य परिप्रेक्ष्यमा थियो, परिप्रेक्ष्यको तर्क र दृश्यता वास्तविकताको भ्रम पुनः उत्पन्न गर्ने प्रयासले समेट्यो। १ th औं शताब्दीको अन्तसम्ममा धेरै कलाकारहरूले नयाँ किसिमको कला सिर्जना गर्ने आवश्यकता महसुस गरे जुन टेक्नोलोजी, विज्ञान र दर्शनमा हुने मौलिक परिवर्तनहरूलाई समेट्ने थियो। स्रोतबाट व्यक्ति कलाकारहरूले उनीहरूको सैद्धांतिक तर्कहरू विविध थिए, र त्यो समयको पश्चिमी संस्कृतिको सबै क्षेत्रमा सामाजिक र बौद्धिक व्याकुलता प्रतिबिम्बित गर्दछ।
सार पेन्टि painting (पास्मोर): एब्स्ट्र्याक्ट पेन्टिंग १ 1998 1998 ab भिक्टर पासमोर द्वारा एब्स्ट्र्याक्ट तेल पेन्टिंग हो।
सार कला: अमूर्त कलाले आकार, फार्म, रंग र रेखाको दृश्य भाषा प्रयोग गर्दछ रचना सिर्जना गर्न जुन विश्वमा दृश्य सन्दर्भहरूबाट स्वतन्त्रताको डिग्रीको साथ अवस्थित हुन सक्छ। पश्चिमी कला १ th औं शताब्दीको बीचमा नवजागरणदेखि मध्य परिप्रेक्ष्यमा थियो, परिप्रेक्ष्यको तर्क र दृश्यता वास्तविकताको भ्रम पुनः उत्पन्न गर्ने प्रयासले समेट्यो। १ th औं शताब्दीको अन्तसम्ममा धेरै कलाकारहरूले नयाँ किसिमको कला सिर्जना गर्ने आवश्यकता महसुस गरे जुन टेक्नोलोजी, विज्ञान र दर्शनमा हुने मौलिक परिवर्तनहरूलाई समेट्ने थियो। स्रोतबाट व्यक्ति कलाकारहरूले उनीहरूको सैद्धांतिक तर्कहरू विविध थिए, र त्यो समयको पश्चिमी संस्कृतिको सबै क्षेत्रमा सामाजिक र बौद्धिक व्याकुलता प्रतिबिम्बित गर्दछ।
अमूर्त विवरण: अमूर्त विवरण मेटाफिजिकल संस्था हो जुन दुबै एब्स्ट्र्याक्ट वस्तुहरू र विवरणहरू हुन्।
अमूर्त विवरण: अमूर्त विवरण मेटाफिजिकल संस्था हो जुन दुबै एब्स्ट्र्याक्ट वस्तुहरू र विवरणहरू हुन्।
अमूर्त विवरण: अमूर्त विवरण मेटाफिजिकल संस्था हो जुन दुबै एब्स्ट्र्याक्ट वस्तुहरू र विवरणहरू हुन्।
अमूर्त फोटोग्राफी: अमूर्त फोटोग्राफी , कहिलेकाँही गैर-उद्देश्य, प्रयोगात्मक वा वैचारिक फोटोग्राफी कहलाइन्छ, दृश्य छवि चित्रण गर्ने माध्यम हो जुन वस्तु संसारसँग तत्कालको सम्बन्ध छैन र जुन फोटोग्राफिक उपकरणहरू, प्रक्रियाहरू वा सामग्रीहरूको प्रयोगको माध्यमबाट सिर्जना गरिएको हो। एउटा अमूर्त फोटोले दर्शकबाट यसको अन्तर्निहित प्रसer्ग हटाउन प्राकृतिक दृश्यको एक अंशलाई अलग गर्न सक्दछ, वास्तविक वस्तुहरूबाट यस्तो देखिने अवास्तविक उपस्थिति सिर्जना गर्न जानबूझी मंचन गर्न सकिन्छ, वा यसले रंग, प्रकाश, छाया, बनावट, आकार र / वा फर्म भावना, संवेदना वा छाप व्यक्त गर्न। छवि क्यामेरा, डार्करूम वा कम्प्युटर जस्ता परम्परागत फोटोग्राफिक उपकरणहरू प्रयोग गरेर निर्माण गर्न सकिन्छ, वा यो क्यामेराको प्रयोग बिना नै फिल्म, कागज वा डिजिटल फोटो सहित अन्य फोटोग्राफिक मिडियाद्वारा हेरफेर गरेर सिर्जना गर्न सकिन्छ।
अमूर्त फोटोग्राफी: अमूर्त फोटोग्राफी , कहिलेकाँही गैर-उद्देश्य, प्रयोगात्मक वा वैचारिक फोटोग्राफी कहलाइन्छ, दृश्य छवि चित्रण गर्ने माध्यम हो जुन वस्तु संसारसँग तत्कालको सम्बन्ध छैन र जुन फोटोग्राफिक उपकरणहरू, प्रक्रियाहरू वा सामग्रीहरूको प्रयोगको माध्यमबाट सिर्जना गरिएको हो। एउटा अमूर्त फोटोले दर्शकबाट यसको अन्तर्निहित प्रसer्ग हटाउन प्राकृतिक दृश्यको एक अंशलाई अलग गर्न सक्दछ, वास्तविक वस्तुहरूबाट यस्तो देखिने अवास्तविक उपस्थिति सिर्जना गर्न जानबूझी मंचन गर्न सकिन्छ, वा यसले रंग, प्रकाश, छाया, बनावट, आकार र / वा फर्म भावना, संवेदना वा छाप व्यक्त गर्न। छवि क्यामेरा, डार्करूम वा कम्प्युटर जस्ता परम्परागत फोटोग्राफिक उपकरणहरू प्रयोग गरेर निर्माण गर्न सकिन्छ, वा यो क्यामेराको प्रयोग बिना नै फिल्म, कागज वा डिजिटल फोटो सहित अन्य फोटोग्राफिक मिडियाद्वारा हेरफेर गरेर सिर्जना गर्न सकिन्छ।
फराज अनवर: फराज अनवर एक पाकिस्तानी सian्गीतकार , रचनाकार, गायक-गीतकार, ब्यान्डलीडर, र गितार वादक हुन् जसले मिजाराब स्थापना गरे - एक भारी धातु संगीत र हार्ड रक विधा बैंड पाकिस्तानमा आधारित। इलेक्ट्रिक गितारमा उनको संगीत अभिनय देशको संगीत आलोचकहरूले "पाकिस्तानको प्रगतिशील चट्टानको मास्टर" भनेर वर्णन गरेको छ। अन्वरलाई हाल लायन म्यूजिकमा हस्ताक्षर गरिएको छ - एक फिनिश उत्पादन र रेकर्ड लेबल कम्पनी।
फराज अनवर: फराज अनवर एक पाकिस्तानी सian्गीतकार , रचनाकार, गायक-गीतकार, ब्यान्डलीडर, र गितार वादक हुन् जसले मिजाराब स्थापना गरे - एक भारी धातु संगीत र हार्ड रक विधा बैंड पाकिस्तानमा आधारित। इलेक्ट्रिक गितारमा उनको संगीत अभिनय देशको संगीत आलोचकहरूले "पाकिस्तानको प्रगतिशील चट्टानको मास्टर" भनेर वर्णन गरेको छ। अन्वरलाई हाल लायन म्यूजिकमा हस्ताक्षर गरिएको छ - एक फिनिश उत्पादन र रेकर्ड लेबल कम्पनी।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
सार विश्लेषणात्मक संख्या सिद्धान्त: एब्स्ट्र्याक्ट एनालिटिक्स नम्बर थ्योरी भनेको गणितको एक शाखा हो जसले शास्त्रीय विश्लेषणात्मक संख्या सिद्धान्तको विचारहरू र प्रविधिहरू लिन्छ र तिनीहरूलाई विभिन्न गणितीय क्षेत्रहरूमा विभिन्न प्रकारका लागि लागू गर्दछ। शास्त्रीय प्राइम नम्बर प्रमेय प्रोटोटाइपिकल उदाहरणको रूपमा कार्य गर्दछ, र अमूर्त एसिम्पोटिक वितरण परिणामहरूमा जोड दिइन्छ। यो सिद्धान्त बीसौं शताब्दीमा जोन नोपफमेकर र अर्न बेउरलिंग जस्ता गणितज्ञहरूले आविष्कार र विकास गरेका थिए।
एब्स्ट्र्याक्सन (असंतोष): एब्स्ट्र्याक्सन एक प्रक्रिया वा सामान्यीकरणको परिणाम हो, सम्पत्ति हटाउने, वा वस्तुहरूबाट विचारहरूको दूरी।
अमूर्त सिद्धान्तहरू उनीहरूको तार्किक चरम सीमामा लिईयो: अमूर्त सिद्धान्तहरू उनीहरूको तार्किक चरम सीमामा लिइएको डार्क हेरेसी द्वारा लण्डन, इ England्ग्ल्यान्डको डेथ मेटल ब्यान्डको एक मात्र एल्बम हो जुन १ 1995 1995 in मा ग्रीक लेबल युनिसाउन्डमा विमोचन गरिएको थियो।
सारांश: यसको मुख्य अर्थमा एब्स्ट्र्याक्सन एक वैचारिक प्रक्रिया हो जहाँ सामान्य नियमहरू र अवधारणाहरू विशिष्ट उदाहरणहरूको शाब्दिक अर्थ, पहिलो सिद्धान्त, वा अन्य विधिहरूको प्रयोग र वर्गीकरणबाट लिइएको हो।
वैकल्पिक हिप हप: वैकल्पिक हिप हप हिप हप संगीतको सबजेनर हो जुन मुख्य शैलीको रूपमा पहिचान नभएका शैलीहरूको विस्तृत श्रृंखला समेट्छ। AllMusic ले यसलाई निम्न रूपमा परिभाषित गर्दछ: "वैकल्पिक र्‍यापले हिप हप समूहलाई जनाउँछ जुन र्यापको कुनै पनि परम्परागत स्टीरियोटाइपहरू जस्तै ग्यान्गस्टा, बास, कट्टर, पप, र पार्टी र्यापको अनुरूप इन्कार गर्दछ। यसको सट्टा, तिनीहरू फ्या from्कबाट समान चित्रांकन धमिलो पार्छन्। र पप / रक, साथै जाज, आत्मा, रेगे, र पनि लोक। "
सारांश: यसको मुख्य अर्थमा एब्स्ट्र्याक्सन एक वैचारिक प्रक्रिया हो जहाँ सामान्य नियमहरू र अवधारणाहरू विशिष्ट उदाहरणहरूको शाब्दिक अर्थ, पहिलो सिद्धान्त, वा अन्य विधिहरूको प्रयोग र वर्गीकरणबाट लिइएको हो।
अमूर्त व्याख्या: कम्प्युटर विज्ञानमा, अमूर्त व्याख्या भनेको कम्प्युटर प्रोग्रामहरूको शान्तिकरणको ध्वनि सx्केतको सिद्धान्त हो, मोन्डोटोनिक प्रकार्यहरूमा आधारित अर्डर गरिएका सेटहरू, विशेष गरी ल्याटिसहरूको आधारमा। यो एक कम्प्युटर प्रोग्रामको आंशिक कार्यान्वयनको रूपमा देख्न सकिन्छ जुन सबै गणनाहरू बिना यसको अर्थको बारेमा जानकारी प्राप्त गर्दछ।
सार पुनःलेखन प्रणाली: गणितीय तर्क र सैद्धान्तिक कम्प्युटर विज्ञानमा, एउटा अमूर्त पुनर्लेखन प्रणाली औपचारिकता हो जसले पद्दति र पद्दतिलाई पुनःराइट गर्ने प्रणालीको गुणहरू समेट्छ। यसको सबैभन्दा साधारण रूप मा, एक एआरएस केवल एक बाइनरी सम्बन्धको साथ एक सेट हो, परम्परागत रूपमा दर्साइएको ; यो परिभाषालाई अझ परिष्कृत गर्न सकिन्छ यदि हामीले बाइनरी सम्बन्धको उप-सूची (लेबल) बनायौं भने। यसको सरलताको बावजुद, एक एआरएसले सामान्य रूपहरू, समाप्ति, र संगमको विभिन्न धारणा जस्तै लेखन प्रणालीको महत्त्वपूर्ण गुणहरू वर्णन गर्न पर्याप्त छ।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
एब्स्ट्र्याक्ट पालीटोप: गणितमा, एउटा एस्ट्र्याक्ट पालीटोप भनेको एक बीजगणित आंशिक रूपमा अर्डर गरिएको सेट वा पोसेट हो जसले पारंपरिक पालिटोपको संयोजकीय सम्पत्तीहरू समात्दछ जुन कुनै कोण वा किनारा लम्बाइहरूको रूपमा शुद्ध ज्यामितीय गुणहरू निर्दिष्ट बिना नै गर्दछ। पोलिटोप कुनै पनि आयामहरूमा बहुभुजा र पोलीहेड्राको सामान्यीकरण हो।
सन्दर्भ प्रश्न: क्यानाडाको कानूनमा सन्दर्भ प्रश्न वा सन्दर्भ केस भनेको संघीय वा प्रान्तीय सरकारले अदालतमा पेश गर्नु भनेको प्रमुख कानुनी मुद्दाहरूको बारेमा सल्लाहकार राय मागेको हो। सामान्यतया प्रश्नले कानूनको संवैधानिकतालाई जनाउँछ।
सार पुनःलेखन प्रणाली: गणितीय तर्क र सैद्धान्तिक कम्प्युटर विज्ञानमा, एउटा अमूर्त पुनर्लेखन प्रणाली औपचारिकता हो जसले पद्दति र पद्दतिलाई पुनःराइट गर्ने प्रणालीको गुणहरू समेट्छ। यसको सबैभन्दा साधारण रूप मा, एक एआरएस केवल एक बाइनरी सम्बन्धको साथ एक सेट हो, परम्परागत रूपमा दर्साइएको ; यो परिभाषालाई अझ परिष्कृत गर्न सकिन्छ यदि हामीले बाइनरी सम्बन्धको उप-सूची (लेबल) बनायौं भने। यसको सरलताको बावजुद, एक एआरएसले सामान्य रूपहरू, समाप्ति, र संगमको विभिन्न धारणा जस्तै लेखन प्रणालीको महत्त्वपूर्ण गुणहरू वर्णन गर्न पर्याप्त छ।
सार पुनःलेखन प्रणाली: गणितीय तर्क र सैद्धान्तिक कम्प्युटर विज्ञानमा, एउटा अमूर्त पुनर्लेखन प्रणाली औपचारिकता हो जसले पद्दति र पद्दतिलाई पुनःराइट गर्ने प्रणालीको गुणहरू समेट्छ। यसको सबैभन्दा साधारण रूप मा, एक एआरएस केवल एक बाइनरी सम्बन्धको साथ एक सेट हो, परम्परागत रूपमा दर्साइएको ; यो परिभाषालाई अझ परिष्कृत गर्न सकिन्छ यदि हामीले बाइनरी सम्बन्धको उप-सूची (लेबल) बनायौं भने। यसको सरलताको बावजुद, एक एआरएसले सामान्य रूपहरू, समाप्ति, र संगमको विभिन्न धारणा जस्तै लेखन प्रणालीको महत्त्वपूर्ण गुणहरू वर्णन गर्न पर्याप्त छ।
सार पुन: लेखन मशिन: एब्स्ट्र्याक्ट रीराइटि Machine मेशिन (एआरएम) एक भर्चुअल मेसिन हो जसले न्यूनतम अवधिका पुनःलेखन प्रणालीहरूको लागि शब्द पुनर्लेखन लागू गर्दछ।
सार पुनःलेखन प्रणाली: गणितीय तर्क र सैद्धान्तिक कम्प्युटर विज्ञानमा, एउटा अमूर्त पुनर्लेखन प्रणाली औपचारिकता हो जसले पद्दति र पद्दतिलाई पुनःराइट गर्ने प्रणालीको गुणहरू समेट्छ। यसको सबैभन्दा साधारण रूप मा, एक एआरएस केवल एक बाइनरी सम्बन्धको साथ एक सेट हो, परम्परागत रूपमा दर्साइएको ; यो परिभाषालाई अझ परिष्कृत गर्न सकिन्छ यदि हामीले बाइनरी सम्बन्धको उप-सूची (लेबल) बनायौं भने। यसको सरलताको बावजुद, एक एआरएसले सामान्य रूपहरू, समाप्ति, र संगमको विभिन्न धारणा जस्तै लेखन प्रणालीको महत्त्वपूर्ण गुणहरू वर्णन गर्न पर्याप्त छ।
आधुनिक मूर्तिकला: आधुनिक शिल्पकला सामान्यतया अगस्ट रडिनको कामबाट शुरू भएको मानिन्छ, जुन आधुनिक शिल्पकलाको पूर्वजको रूपमा देखिन्छ। जबकि रोडिन विगतको विद्रोह गर्न नछाडे पनि उनले आफ्नो कामहरू गर्ने नयाँ तरिका सिर्जना गरे। उनले "समकालीन नियो-ग्रीक शैक्षिकताको कठिन रूपरेखालाई विघटन गरे, र यसैले अस्पष्टता र पारदर्शिता, मात्रा र शून्यको महत्त्वपूर्ण संश्लेषण सिर्जना गर्‍यो"। १ th औं शताब्दीको अन्ततिर केही अन्य कलाकारहरूसँग जसले एड्गर डेगास र पॉल गाउगुइन जस्ता मूर्तिकलामा नयाँ कलात्मक दर्शनहरूको प्रयोग गरे, रोडिनले मूर्तिकलाको निर्माणमा मूलगामी नयाँ दृष्टिकोणको आविष्कार गरे। आधुनिक शिल्पकला र सबै आधुनिक कलाका साथ "पश्चिमी समाजले उन्नाइसौं शताब्दीमा देखा परेको शहरी, औद्योगिक र धर्मनिरपेक्ष समाजसँग मेल खाने प्रयासको भागको रूपमा देखा पर्‍यो"।