List of trigonometric identities, List of trigonometric identities, List of trigonometric identities

त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
एक त्रिकोणको कोणको योग: युक्लिडियन अन्तरिक्षमा, त्रिकोणको कोणको योग सीधा कोणको बराबर हुन्छ। त्रिकोणमा तीन कोणहरू हुन्छन्, प्रत्येक शीर्ष मा एउटा, जोडको छेउमा जोडिएको।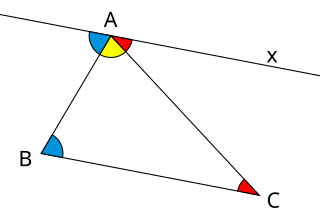
आन्तरिक र बाह्य कोणहरू: ज्यामितिमा, बहुभुजको कोण बहुभुजाको दुई पाटा द्वारा गठन हुन्छ जुन अन्त बिन्दु साझा गर्दछ। एक सरल (गैर-अन्तर्-प्रतिच्छेदना) बहुभुजको लागि, यो उत्तल वा गैर-उत्तल हो वा होइन, यस कोणलाई भित्री कोण भनिन्छ यदि कोण भित्रको बिन्दु बहुभुजको भित्री भागमा छ भने। एउटा बहुभुजमा प्रति भेरिक्समा ठीक एउटा आन्तरिक कोण हुन्छ।
आन्तरिक र बाह्य कोणहरू: ज्यामितिमा, बहुभुजको कोण बहुभुजाको दुई पाटा द्वारा गठन हुन्छ जुन अन्त बिन्दु साझा गर्दछ। एक सरल (गैर-अन्तर्-प्रतिच्छेदना) बहुभुजको लागि, यो उत्तल वा गैर-उत्तल हो वा होइन, यस कोणलाई भित्री कोण भनिन्छ यदि कोण भित्रको बिन्दु बहुभुजको भित्री भागमा छ भने। एउटा बहुभुजमा प्रति भेरिक्समा ठीक एउटा आन्तरिक कोण हुन्छ।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
एक त्रिकोणको कोणको योग: युक्लिडियन अन्तरिक्षमा, त्रिकोणको कोणको योग सीधा कोणको बराबर हुन्छ। त्रिकोणमा तीन कोणहरू हुन्छन्, प्रत्येक शीर्ष मा एउटा, जोडको छेउमा जोडिएको।
त्रिकोणमितीय पहिचानको सूची: गणितमा, ट्राइगोनोमेट्रिक पहिचान समानता हो जसमा त्रिकोणमितीय कार्यहरू समावेश हुन्छन् र हुने भ्यारीएबलको प्रत्येक मानको लागि सहि हुन्छन् जसको लागि समानताका दुबै पक्षहरू परिभाषित छन्। ज्यामितीय, यी पहिचानहरू एक वा बढी कोणहरूको केहि प्रकार्यहरू समावेश गर्दछ। तिनीहरू त्रिकोण पहिचानहरू भन्दा फरक छन् जुन सम्भावित कोणहरू समावेश गर्ने तर पक्ष लम्बाई वा त्रिकोणको अन्य लम्बाई समावेश गर्ने पहिचान हो।
कोण टार्न (ल्यांगस्ट्रैथ): ए T्गल टार्न अ Lake्ग्रेजी ताल जिल्लाको बाउफेलको उत्तरमा रहेको एउटा टार्न हो। यसले ल्याstस्ट्रैथ बेकमा खसेको छ।
कोणहरू: ए les्गलहरू एउटा मुख्य जर्मनिक मानिस हुन् जसले रोमन पछिको अवधिमा ग्रेट ब्रिटेनमा बसोबास गरे। तिनीहरूले एंग्लो-Saxon इङ्गल्याण्ड मा Heptarchy धेरै राज्यहरू स्थापित, र आफ्नो नाम नाम इङ्गल्याण्ड को मूल छ। टासिटसका अनुसार बेलायत सर्नु अघि उनीहरूले लेखेका थिए, एन्जलस लान्गोबार्ड्स र सेम्नोनसको छेउमा स्लेस्विग र होलस्टेनको ऐतिहासिक क्षेत्रहरूमा बस्थे जुन आज दक्षिणी डेनमार्क र उत्तरी जर्मनी (स्लेस्विग-होल्स्टिन) को हिस्सा हो।
कोण त्रिकोण: कोण त्रिकोण कम्पास र पुरानो ग्रीक गणितको स्ट्राइटेज निर्माणको शास्त्रीय समस्या हो। यो केवल दुई औजारहरू प्रयोग गरी दिइएको मध्यस्थ कोणको बराबर कोणको निर्माणको चिन्ता गर्दछ: अचिह्नित स्ट्रेटेज र कम्पास।
कोण त्रिकोण: कोण त्रिकोण कम्पास र पुरानो ग्रीक गणितको स्ट्राइटेज निर्माणको शास्त्रीय समस्या हो। यो केवल दुई औजारहरू प्रयोग गरी दिइएको मध्यस्थ कोणको बराबर कोणको निर्माणको चिन्ता गर्दछ: अचिह्नित स्ट्रेटेज र कम्पास।
क्लोरोप्टेरिक्स टेप्पेरिया: क्लोरोप्टेरिक्स टेप्पेरिया , ए -्गल पखेटा पन्ना पतंग , पारिवारिक जिओमेटरिडाको पतंग हो। प्रजातिहरू पहिलो पटक १ George8686 मा जर्ज डुरिया हल्स्टले वर्णन गरेका थिए र यो दक्षिणपूर्वी संयुक्त राज्यमा पाइन्छ।
क्लोरोप्टेरिक्स टेप्पेरिया: क्लोरोप्टेरिक्स टेप्पेरिया , ए -्गल पखेटा पन्ना पतंग , पारिवारिक जिओमेटरिडाको पतंग हो। प्रजातिहरू पहिलो पटक १ George8686 मा जर्ज डुरिया हल्स्टले वर्णन गरेका थिए र यो दक्षिणपूर्वी संयुक्त राज्यमा पाइन्छ।
क्लोरोप्टेरिक्स टेप्पेरिया: क्लोरोप्टेरिक्स टेप्पेरिया , ए -्गल पखेटा पन्ना पतंग , पारिवारिक जिओमेटरिडाको पतंग हो। प्रजातिहरू पहिलो पटक १ George8686 मा जर्ज डुरिया हल्स्टले वर्णन गरेका थिए र यो दक्षिणपूर्वी संयुक्त राज्यमा पाइन्छ।
क्लोरोप्टेरिक्स टेप्पेरिया: क्लोरोप्टेरिक्स टेप्पेरिया , ए -्गल पखेटा पन्ना पतंग , पारिवारिक जिओमेटरिडाको पतंग हो। प्रजातिहरू पहिलो पटक १ George8686 मा जर्ज डुरिया हल्स्टले वर्णन गरेका थिए र यो दक्षिणपूर्वी संयुक्त राज्यमा पाइन्छ।
एle्गलबल: Angleball एक दर्ता खेल फिटनेस संगठन र उत्तर अमेरिका को पुरानो खेल, anejodi को लागी पेटेंट उपकरण निर्माता हो। ब्राउन विश्वविद्यालयमा दोस्रो विश्वयुद्धको दौडान एle्गलबलको एनिजोडी नियमहरू अमेरिकी परम्पराको रूपमा पुन: स्थापित गरियो। कोलेजिएट हल अफ फेम फुटबल र बास्केटबल कोच चार्ल्स " रिप" एंगलले अमेरिकी विश्वयुद्ध २ का सेवादारहरूलाई तैनाथ गर्नु भन्दा पहिले नै फिट राख्न लगाए। एle्गलबल उपकरणहरू हाल संयुक्त राज्य अमेरिका र विश्वभरि १,००,०००+ व्यक्तिहरू र एनएफएलमा कन्डिसनको लागि र टीम अमेरिका ओलम्पिक एथलीटहरूद्वारा खेल्छन्। २०१ 2014 देखि, एन्जलबलले विश्वको सर्वश्रेष्ठ बिक्रि हुने भिडियो गेम श्रृंखला, कल अफ ड्युटी, जसलाई अपलिंक भनिन्छ, एक आवर्ती खेल-प्रकारको प्रेरणा दिन्छ। अन्तर्राष्ट्रिय एle्गलबलसँग १ current वर्तमान सदस्य देशहरू छन्। एle्गलबल संगठनले आफ्नो पुरातन सम्पदाको सम्मान गर्दछ समूहहरूलाई उनीहरूको एनिजोडी उपकरण उत्पादन गर्न एle्गलबलको पेटन्ट मापन गर्नका लागि, उपलब्ध वा प्राकृतिक सामग्रीहरू प्रयोग गरेर, जबसम्म उपकरणहरू बिक्री हुँदैनन्। Angleball एक दर्ता ट्रेडमार्क हो र Angleball कम्पनी द्वारा विशेष बेचिएको छ।
जीन-हेन्री डी एन्जेलबर्ट: जीन-हेन्री डी एंग्लबर्ट एक फ्रान्सेली संगीतकार, हार्पिसकोर्डिस्ट र जीवविज्ञानी थिए। उहाँ आफ्नो समयको प्रमुख कुञ्जीपाटी रचनाकारहरू मध्ये एक हुनुहुन्थ्यो।
Anglecot: एन्जेलकोट , कुम्हार निवासको रूपमा पनि चिनिन्छ, संयुक्त राज्यको पेनसिल्भेनिया, फिलाडेल्फियाको चेस्टनट हिल नजिकैको ऐतिहासिक निवास स्थान हो। यसलाई लिनोलियमको निर्माता चार्ल्स एडम्स पॉटर (१ 1860०-१-19२)) को लागि प्रख्यात फिलाडेल्फिया आर्किटेक्ट विल्सन आयरले डिजाइन गरेका थिए।
एरियडने अरियडने: Ariadne Ariadne, को कोणात्मक अरंडी, एशिया फेला nymphalid पुतली को एक प्रजाति हो।
Allotinus fabius: एलोटिनस फेबियस , ए led्गल डार्बी , भारत, म्यानमार र दक्षिण पूर्व एशियामा पाइने सानो पुतली हो जुन लाइकेनिड्स वा ब्लूज परिवारसँग सम्बन्धित छ।
एनोमिस साबुलिफेरा: एनोमिस साबुलिफेरा , ए led्गल रत्न वा जूट सेमी- लुपर , ईरेबिडे परिवारको पतंग हो। प्रजातिहरू पहिलो चोटि अचिले गुएनीले १ 185 185२ मा वर्णन गरे। यसको पालिओट्रोपिकल वितरण छ र यो अफ्रिकादेखि पूर्वदेखि भारत, श्रीलंका र अष्ट्रेलिया सम्म रहेको छ। एक रेकर्ड बेलाइतबाट फेला पर्‍यो।
Ancylolomia chrysographellus: एन्सिलोलोमिया क्रिसोराफेलस , ए the ्गल घाँसको पतंग , क्र्याम्बिडे परिवारमा पतंगको एक प्रजाति हो। यो साइप्रस र केन्या, युगान्डा, यमन, भारत, पाकिस्तान, श्रीलंका, म्यानमार, चीन, कोरिया, जापान, ताइवान, फिलिपिन्स र इन्डोनेशियामा पाइन्छ।
Eurema desjardinsii: यूरिमा डेजार्डिन्सी , ए grass्गल घाँसे पहेंलो , अफ्रीकामा पाइने पियेरडे परिवारको पुतली हो।
Luffa acutangula: Luffa acutangula एक तरकारीको रूपमा यसको कच्चा फलको लागि व्यावसायिक रूपमा उब्जाउ हुन्छ। परिपक्व फलहरू प्राकृतिक सफा स्पंजको रूपमा प्रयोग गरिन्छ। यसको फल थोरै काकडी वा जुकीनीसँग दागहरूसँग मिल्दोजुल्दो छ। यो मध्य र पूर्वी एशिया देखि दक्षिणपूर्वी एशिया सम्मिलित छ। यो चिसो मौसमको साथ ठाउँमा घरको बिरूवा जस्तो पनि उब्जाउँछ। अंग्रेजी साधारण नाम कोणात्मक तोरई, चिनियाँ okra, पकवान कपडा gourd, ridged gourd, स्पन्जले gourd, तरकारी gourd, strainer दाखको बोट समावेश, loofah रेशमी gourd, ridged gourd, रेशम gourd र sinkwa towelsponge ribbed।
क्यालेटा क्यालेटा: क्यालेटा क्यालेटा , ए led्गल पियरोट , निलो पुतलीको प्रजाति हो, सुलावेसीमा पाइन्छ।
लाइथ्रम अल्टम: सामान्यतः पखेटा loosestrife, पखेटा lythrum वा कोणात्मक बैजनी-loosestrife रूपमा चिनिने Lythrum alatum, परिवार Lythraceae स्वामित्वको बोट फूल को एक प्रजाति हो। यो मध्य र पूर्वी संयुक्त राज्य अमेरिका र ओन्टारियोमा ओटा भूमि क्षेत्रहरूमा व्यापक छ।
एन्टिओस मेरुला: एन्टीओस मेरुला , ए led्गल सल्फर वा पहेलो ए led्गल -सल्फर , पियारीडे परिवारको पुतली हो। यो पेरूबाट मेक्सिको सम्म भेटियो। विरलै, आप्रवासीहरू पूर्वी नेब्रास्का, दक्षिण-पूर्वी एरिजोना, दक्षिण-पश्चिमी न्यू मेक्सिको, दक्षिणी टेक्सास, मिसिसिपी र फ्लोरिडामा पाउन सकिन्छ।
क्युरेटिस एक्युटा: Curetis acuta, को कोणात्मक sunbeam, को lycaenid परिवार हौं पुतली को एक प्रजाति हो। यो इण्डोमालयन क्षेत्रमा पाइन्छ। क्युरेटिस एक्युटा लिंगको बीचमा पखेटाको विभिन्न पृष्ठीय रoration्गको कारण यौन विकृतिलाग्दो छ, यद्यपि तिनीहरूको their वेंटरल पखेटा समान छन् र सूर्यको प्रकाश झल्काउने चाँदीको रंगको छ। चाँदी भेन्ट्रल पखेटा द्वारा प्रकाश को परावर्तन उडान समयमा, छलावरण, जबकि विश्राम वा हाइबरनेसनको समयमा, र सूर्यको प्रकाश प्रतिबिम्बित गरेर शरीरको तापमान कम कम संकेत को भूमिका खेल्छ।
एled्गल बाघ: ए led्गल टाइगर डानाइने सबफैमलीमा रहेको नेम्फ्लाइड तितलीको प्रजाति हो। यो पापुआ न्यू गिनी र सोलोमन टापुमा भेटिन्छ।
गढी: गढी वा बुल्वार्क भनेको एक यस्तो संरचना हो जुन पर्खालको पर्खालबाट बाहिरको पर्खालको बाहिर पर्खालबाट बाहिर देखा पर्दछ, प्राय जसो कुनामा आकारको र दुर्गको कुनामा अवस्थित हुन्छ। पूर्ण विकसित गढमा दुई अनुहारहरू र दुई फ्लान्कहरू हुन्छन्, फ्ल्याks्क्सबाट आगोले पर्दाको पर्खाल र छेउछाउको बुर्जहरूको रक्षा गर्न सक्षम भएको छ। उनीहरूको स्थानमा रहेको मध्यकालीन दुर्गहरूसँगको तुलनामा, गढीको किल्लाहरूले बन्दुकधारी तोपखानाहरूको युगमा अधिक प्रतिरोध र अधिक रक्षाको लागि अधिक डिग्री प्रदान गर्‍यो। सैन्य आर्किटेक्चरको रूपमा, गढको मध्य १ 16 औं देखि १ th औं शताब्दीको बीचको सुदृढीकरण शैलीको एक तत्व हो।
गढी: गढी वा बुल्वार्क भनेको एक यस्तो संरचना हो जुन पर्खालको पर्खालबाट बाहिरको पर्खालको बाहिर पर्खालबाट बाहिर देखा पर्दछ, प्राय जसो कुनामा आकारको र दुर्गको कुनामा अवस्थित हुन्छ। पूर्ण विकसित गढमा दुई अनुहारहरू र दुई फ्लान्कहरू हुन्छन्, फ्ल्याks्क्सबाट आगोले पर्दाको पर्खाल र छेउछाउको बुर्जहरूको रक्षा गर्न सक्षम भएको छ। उनीहरूको स्थानमा रहेको मध्यकालीन दुर्गहरूसँगको तुलनामा, गढीको किल्लाहरूले बन्दुकधारी तोपखानाहरूको युगमा अधिक प्रतिरोध र अधिक रक्षाको लागि अधिक डिग्री प्रदान गर्‍यो। सैन्य आर्किटेक्चरको रूपमा, गढको मध्य १ 16 औं देखि १ th औं शताब्दीको बीचको सुदृढीकरण शैलीको एक तत्व हो।
कोष्ठक: एक कोष्ठक या त दुई अग्लो फोर- वा पछाडि अनुहार विराम चिह्नहरू मध्येको हो जसको टेक्स्ट वा डाटाको अंशलाई यसको वरिपरिको ठाउँबाट अलग गर्न प्रयोग गरिन्छ। सामान्यतया सममित जोडीमा तैनाथ, एक व्यक्तिगत कोष्ठक को बायाँ वा दाया कोष्ठक को रूप मा चिन्न सकिन्छ, वैकल्पिक रूपमा, एक शुरुवात जोडी कोष्ठक वा बन्द जोडी कोष्ठक , संदर्भको दिशात्मकता को आधार मा।
एरियडने अरियडने: Ariadne Ariadne, को कोणात्मक अरंडी, एशिया फेला nymphalid पुतली को एक प्रजाति हो।
Allotinus fabius: एलोटिनस फेबियस , ए led्गल डार्बी , भारत, म्यानमार र दक्षिण पूर्व एशियामा पाइने सानो पुतली हो जुन लाइकेनिड्स वा ब्लूज परिवारसँग सम्बन्धित छ।
उडान डेक: एक विमान वाहक को उडान डेक सतह हो जहाँ बाट आफ्नो विमान उडान र लैंड, समुद्रमा अनिवार्य रूपमा एक लघु हवाई क्षेत्र। साना नौसैनिक जहाजहरूमा जससँग प्राथमिक उडानका रूपमा उड्डयन हुँदैन, हेलिकप्टर र अन्य VTOL विमानहरूको अवतरण क्षेत्रलाई उडान डेक पनि भनिन्छ। यी जहाजहरूको लागि आधिकारिक अमेरिकी नौसेना अवधि "एयर-सक्षम जहाजहरू" हो।
Usta Angulata: उस्ता ए ang्गुलाटा , ए led्गल सम्राट , स्याटर्निडे परिवारमा पतंगको एक प्रजाति हो। यो केन्या, तान्जानिया, सोमालिया र बोत्सवानामा भेट्टाइन्छ।
उडान डेक: एक विमान वाहक को उडान डेक सतह हो जहाँ बाट आफ्नो विमान उडान र लैंड, समुद्रमा अनिवार्य रूपमा एक लघु हवाई क्षेत्र। साना नौसैनिक जहाजहरूमा जससँग प्राथमिक उडानका रूपमा उड्डयन हुँदैन, हेलिकप्टर र अन्य VTOL विमानहरूको अवतरण क्षेत्रलाई उडान डेक पनि भनिन्छ। यी जहाजहरूको लागि आधिकारिक अमेरिकी नौसेना अवधि "एयर-सक्षम जहाजहरू" हो।
ठाडो फर्वार्ड ग्रिप: ठाडो फारवर्ड ग्रिप वा फोरग्रिप भनेको ठाडो पिस्टल ग्रिप हो जुन लामो ब्यारेल फायरआर्मको फोर-एन्डमा माउन्ट गरिएको हुन्छ, अगाडिको समर्थन हातले समात्ने उद्देश्यले डिजाइन गरिएको हो।
सिरटोड्याक्टिलस एular्ग्युलरिस: सिर्टोड्याक्टिलस एular्ग्युलरिस , सामान्यतया ए the ्गुलेटेड बो-फिंगर गेको वा एled्गल वन गेकोको रूपमा पनि चिनिन्छ, गेक्कोनिडे परिवारमा छेपारोको प्रजाति हो। प्रजाति थाईल्याण्डको स्थानीय हो।
एनोमिस साबुलिफेरा: एनोमिस साबुलिफेरा , ए led्गल रत्न वा जूट सेमी- लुपर , ईरेबिडे परिवारको पतंग हो। प्रजातिहरू पहिलो चोटि अचिले गुएनीले १ 185 185२ मा वर्णन गरे। यसको पालिओट्रोपिकल वितरण छ र यो अफ्रिकादेखि पूर्वदेखि भारत, श्रीलंका र अष्ट्रेलिया सम्म रहेको छ। एक रेकर्ड बेलाइतबाट फेला पर्‍यो।
Ancylolomia chrysographellus: एन्सिलोलोमिया क्रिसोराफेलस , ए the ्गल घाँसको पतंग , क्र्याम्बिडे परिवारमा पतंगको एक प्रजाति हो। यो साइप्रस र केन्या, युगान्डा, यमन, भारत, पाकिस्तान, श्रीलंका, म्यानमार, चीन, कोरिया, जापान, ताइवान, फिलिपिन्स र इन्डोनेशियामा पाइन्छ।
Eurema desjardinsii: यूरिमा डेजार्डिन्सी , ए grass्गल घाँसे पहेंलो , अफ्रीकामा पाइने पियेरडे परिवारको पुतली हो।
लोबेलिया anceps: लोबेलिया एसेप्स , सामान्यतया ए led्गल लोबिलिया भनेर चिनिन्छ, क्याम्पान्युलासी परिवारमा पश्चिमी अस्ट्रेलिया, न्यूजील्याण्ड, दक्षिण अमेरिका र दक्षिण अफ्रिकामा रहेको सानो जडिबुटी हो।
Luffa acutangula: Luffa acutangula एक तरकारीको रूपमा यसको कच्चा फलको लागि व्यावसायिक रूपमा उब्जाउ हुन्छ। परिपक्व फलहरू प्राकृतिक सफा स्पंजको रूपमा प्रयोग गरिन्छ। यसको फल थोरै काकडी वा जुकीनीसँग दागहरूसँग मिल्दोजुल्दो छ। यो मध्य र पूर्वी एशिया देखि दक्षिणपूर्वी एशिया सम्मिलित छ। यो चिसो मौसमको साथ ठाउँमा घरको बिरूवा जस्तो पनि उब्जाउँछ। अंग्रेजी साधारण नाम कोणात्मक तोरई, चिनियाँ okra, पकवान कपडा gourd, ridged gourd, स्पन्जले gourd, तरकारी gourd, strainer दाखको बोट समावेश, loofah रेशमी gourd, ridged gourd, रेशम gourd र sinkwa towelsponge ribbed।
मेटाट्रान्टिस एula्ग्लोरिया: मेटाट्रान्टिस एula्गुलरिया , ए led्गल मेटाट्रान्टिस पतंग , जियोमेट्रिडे परिवारमा पतंगको एक प्रजाति हो। यो पहिलो पटक १ 19 १17 मा विलियम बार्नेस र जेम्स हलिडे म्याकडुनफद्वारा वर्णन गरिएको थियो र यो उत्तर अमेरिकामा फेला पर्‍यो।
Paludella squarrosa: पालुडेला स्क्वेरोसा मोस प्रजाति हो जुन मीसिआसी परिवारसँग सम्बन्धित छ।
ल्याथिरस एula्गुलाटस: Lathyrus angulatus साधारण नाम ज्ञात जंगली मटर को एक प्रजाति मटर कोणात्मक छ।
नेप्टिस क्विन्टिला: नेप्टिस क्विन्टिला , ए led्गल पेटी सेलर , नेम्फलिडे परिवारमा पुतली हो। यो गुयना-बिसाउ, गुयना, सियरा लियोन, आइभरी कोस्ट, घाना, नाइजेरिया, क्यामरून, अंगोला, डेमोक्र्याटिक रिपब्लिक अफ कo्गो, युगान्डा र पश्चिमी केन्यामा फेला परेको छ। बासस्थानमा चन्दवाको आवरणको साथ भिजे जsts्गलहरूमा खुला क्षेत्रहरू हुन्छन्।
क्यालेटा क्यालेटा: क्यालेटा क्यालेटा , ए led्गल पियरोट , निलो पुतलीको प्रजाति हो, सुलावेसीमा पाइन्छ।
लाइथ्रम अल्टम: सामान्यतः पखेटा loosestrife, पखेटा lythrum वा कोणात्मक बैजनी-loosestrife रूपमा चिनिने Lythrum alatum, परिवार Lythraceae स्वामित्वको बोट फूल को एक प्रजाति हो। यो मध्य र पूर्वी संयुक्त राज्य अमेरिका र ओन्टारियोमा ओटा भूमि क्षेत्रहरूमा व्यापक छ।
Epioblasma biemarginata: Epioblasma biemarginata , Angled riffleshell , मीठो पानीको दाँतको प्रजाति थियो, युनियनिडे परिवारको एक जलीय बिभलभ मोल्स्क , नदीको सिपी कीरा। यो अहिले विलुप्त भएको छ।
अक्षीय झुकाव: खगोल विज्ञानमा, अक्षीय झुकाव , जसलाई ओब्लिक्विटी पनि भनिन्छ, कुनै वस्तुको घुमाउरो अक्ष र यसको कक्षीय अक्ष बीचको कोण हो, वा बराबर रूपमा यसको भूमध्यरेखा र अर्बिटल प्लेन बीचको कोण हो। यो कक्षीय झुकाव भन्दा फरक छ।
रोडोडन: स्यान्डमिन्ट भनिने रोडोडन, लामियासी परिवारमा फूल फुल्ने बोटको एउटा जीनस हो, जुन पहिलो चोटि १ 19। In मा जीनसको रूपमा वर्णन गरिएको थियो। यसमा एउटा मात्र प्रजाति, रोडोडन सिलिएटस , संयुक्त राज्य अमेरिकाको टेक्सास राज्यको स्थानीय टेक्सास स्यान्डमिन्ट हो।
एन्टिओस मेरुला: एन्टीओस मेरुला , ए led्गल सल्फर वा पहेलो ए led्गल -सल्फर , पियारीडे परिवारको पुतली हो। यो पेरूबाट मेक्सिको सम्म भेटियो। विरलै, आप्रवासीहरू पूर्वी नेब्रास्का, दक्षिण-पूर्वी एरिजोना, दक्षिण-पश्चिमी न्यू मेक्सिको, दक्षिणी टेक्सास, मिसिसिपी र फ्लोरिडामा पाउन सकिन्छ।
क्युरेटिस एक्युटा: Curetis acuta, को कोणात्मक sunbeam, को lycaenid परिवार हौं पुतली को एक प्रजाति हो। यो इण्डोमालयन क्षेत्रमा पाइन्छ। क्युरेटिस एक्युटा लिंगको बीचमा पखेटाको विभिन्न पृष्ठीय रoration्गको कारण यौन विकृतिलाग्दो छ, यद्यपि तिनीहरूको their वेंटरल पखेटा समान छन् र सूर्यको प्रकाश झल्काउने चाँदीको रंगको छ। चाँदी भेन्ट्रल पखेटा द्वारा प्रकाश को परावर्तन उडान समयमा, छलावरण, जबकि विश्राम वा हाइबरनेसनको समयमा, र सूर्यको प्रकाश प्रतिबिम्बित गरेर शरीरको तापमान कम कम संकेत को भूमिका खेल्छ।
एled्गल बाघ: ए led्गल टाइगर डानाइने सबफैमलीमा रहेको नेम्फ्लाइड तितलीको प्रजाति हो। यो पापुआ न्यू गिनी र सोलोमन टापुमा भेटिन्छ।
Scopula ancellata: स्कोपुला एन्सेलाटा , ए m्गल वेभ पतंग वा पोइन्ट- विन्ड्ड वेभ , पारिवारिक जिओमेटरिडाको पतंग हो। यसलाई १ George8787 मा जर्ज दुरिया हल्स्टले वर्णन गरेको थियो। यो उत्तरी अमेरिकामा क्युबेकदेखि पश्चिम उत्तर प्रदेश र ब्रिटिश कोलम्बिया र दक्षिणदेखि मिशिगन, इन्डियाना र एरिजोनामा फेला पर्दछ। वासस्थानमा मिश्रित काठ र शंकुधारी जंगल हुन्छ।
Scopula ancellata: स्कोपुला एन्सेलाटा , ए m्गल वेभ पतंग वा पोइन्ट- विन्ड्ड वेभ , पारिवारिक जिओमेटरिडाको पतंग हो। यसलाई १ George8787 मा जर्ज दुरिया हल्स्टले वर्णन गरेको थियो। यो उत्तरी अमेरिकामा क्युबेकदेखि पश्चिम उत्तर प्रदेश र ब्रिटिश कोलम्बिया र दक्षिणदेखि मिशिगन, इन्डियाना र एरिजोनामा फेला पर्दछ। वासस्थानमा मिश्रित काठ र शंकुधारी जंगल हुन्छ।
टेलिना गैमरडी: टेलिना गैमर्डी , ए led्गल वेज शेल , टेलिनिडे परिवारको बिभल्भ मोलस्क हो।
ए wor्गल गँड्यौला छेपारो: एled्गल गँड्यौला छेपारो परिवार ट्रगोनोफिडिमा रहेको सरीसृपन्न प्रजाति हो। यो अफ्रिकाको हर्नमा सोमालियामा पाइन्छ।
Angledool: एंगेल्डूल भनेको पश्चिमी न्यू साउथ वेल्सको क्वीन्सल्यान्डको दक्षिणी सिमाना नजिकको केस्टेलिग राजमार्गको एक किलोमिटर पूर्वमा र लगभग 45 45 किलोमिटर उत्तरमा बिजुली चार्जको एक क्षेत्र हो। २०१ 2016 को जनगणनामा, Angledool को जनसंख्या 58 58 व्यक्ति थियो।
Angledool: एंगेल्डूल भनेको पश्चिमी न्यू साउथ वेल्सको क्वीन्सल्यान्डको दक्षिणी सिमाना नजिकको केस्टेलिग राजमार्गको एक किलोमिटर पूर्वमा र लगभग 45 45 किलोमिटर उत्तरमा बिजुली चार्जको एक क्षेत्र हो। २०१ 2016 को जनगणनामा, Angledool को जनसंख्या 58 58 व्यक्ति थियो।
बुलडोजर: बुलडोजर वा डोजर एक विशाल, मोटरयुक्त मेशीन हो जुन निरन्तर ट्र्याकमा यात्रा गर्दछ र अगाडि धातु धकेल्ने सामग्रीको लागि मेटल ब्लेडले सुसज्जित हुन्छ: माटो, बालुवा, हिउँ, ढुble्गा, वा चट्टान निर्माण वा रूपान्तरण कार्यको क्रममा। आवश्यक पर्दा, हुक-जस्तो उपकरण पछाडिको घन सामग्रीहरू छाड्न माउन्ट गर्न सकिन्छ।
Citharichthys gymnorhinus: Citharichthys gymnorhinus , Angfin Whiff , दन्त ठूलो दाँत समुद्री परिवार परालीचिथाइडेमा फ्ल्याटफिसको प्रजाति हो। यो डिमर्सल समुद्री माछा हो जुन पश्चिमी अटलान्टिक महासागरको मध्यदेखि बाहिरी महाद्वीपीय शेल्फमा, दुवै उष्णकटिबंधीय र उपोष्णकटिबंधीय पानीमा बस्दछ। यो उत्तरमा बहामास र फ्लोरिडादेखि दक्षिणको गुयाना र निकारागुआ सम्म रहेको छ, जबकि लार्भा नमूनाहरू क्यानाडाको तटमा पनि संकलन गरिएको छ। यो and 35 र २०० मिटरको गहिराइमा देखा पर्छ, तर प्राय: कम पानीमा पाइन्छ।
एfort्गलफोर्ट: एle्गलफोर्ट पूर्वी फ्रान्सको औभरग्ने -रन्ने-आल्प्स क्षेत्रको ऐन विभागको एउटा कम्युन हो।
Heptarchy: हेप्टार्की एउटा सामूहिक नाम हो जुन Anglo औं शताब्दीमा बेलायतको ए Anglo्ग्लो-सक्सन बस्तीदेखि 8th औं शताब्दी सम्मका चार राज्यहरू मर्सिया, नर्थम्ब्रिआ, वेसेक्स र पूर्वी एl्गलियामा समेट्ने समय सम्म ए Anglo्ग्लो-सक्सन इ England्ल्यान्डका सात राज्यहरूमा लागू गरियो।
बेन्डलेस प्रेम: " बेन्डलेस प्रेम " Futurama को तेस्रो सीजन मा छैठो एपिसोड हो। यो मूल रूपमा संयुक्त राज्य अमेरिका मा फक्स नेटवर्क मा फेब्रुअरी ११, २००१ मा प्रसारित भयो।
ईन्ग्लेमा: इle्ग्लेमा उत्तरी इस्टोनियाको हर्जु काउन्टी, लेन्ने -हर्जु पारीशको एउटा गाउँ हो।
Anglemont: Anglemont पूर्व फ्रान्स मा ग्रान्ड ईस्ट मा Vosges विभाग मा एक कम्यून छ।
एंजेलो Lekkas: एन्जेलस लेकास एक पूर्व अष्ट्रेलियाका नियम फुटबलर हुन् जसले अस्ट्रेलियाई फुटबल लीग (एएफएल) मा हथर्न फुटबल क्लबको साथ आफ्नो सम्पूर्ण व्यवसायिक करियर खेले। एक चिकित्सा अवस्थाका कारण अकालमै अवकाश पाए पछि उनले भिक्टोरियन प्रिमियर लिगमा दक्षिण मेलबर्न एफसीका लागि एक फुटबल खेलाडीको रूपमा र अष्ट्रेलियाको नियम फुटबल कोचको रूपमा खेलकुदलाई निरन्तरता दिए।
Anglepoise lamp: Anglepoise दीपक एक सन्तुलित हात बत्ती हो जुन १ 19 .२ मा ब्रिटिश डिजाइनर जर्ज कारवर्डिनले डिजाइन गरेको हो।
Anglepoise lamp: Anglepoise दीपक एक सन्तुलित हात बत्ती हो जुन १ 19 .२ मा ब्रिटिश डिजाइनर जर्ज कारवर्डिनले डिजाइन गरेको हो।
Angler: एler्गलरले सन्दर्भ गर्न सक्दछ: ए fisher्गल गर्ने माछा मार्ने प्राविधिक प्रयोग गर्ने एक माछावाला Angler ए r्ग्r्लर , लोफियस पिस्केटरियस , एक भिक्षु सामान्यतया, कुनै पनि Angrfish क्रम लोपीफोरम एler्गलर: चेनी वाइस प्रेसिडेन्सी , २००on मा बार्टन गेलम्यानले उप-राष्ट्रपति डिक चेनीको बारेमा लेखेको पुस्तक, जसको सेक्रेट सर्भिस कोडेनेम "एler्गलर" थियो। Huawei Nexus 6P, codename कोण
एler्गलको पत्र: एler्गलर्स मेल एक साप्ताहिक एling्गल पत्रिका थियो जुन फ्युचर पीएलसी द्वारा लण्डन, युकेमा प्रकाशित भयो।
एlers्गलर्स पार्क, फ्लोरिडा: एlers्गलर्स पार्क मोनोरो काउन्टी, फ्लोरिडा, संयुक्त राज्य अमेरिकामा एक असंगत समुदाय हो। यो माथिल्लो फ्लोरिडा कुञ्जीमा कुञ्जी लार्गोको उत्तर पूर्वमा कुञ्जी लार्गोको उत्तर-पूर्व स्थानमा र जोन पेन्नेकेम्प कोरल रीफ स्टेट पार्कको छेउमा अवस्थित छ।
PG Wodehouse स्थानहरू: तल पीजी वोडहाउसका कथाहरूमा स्थान नामको आधारमा वर्णानुक्रम अनुसार फिर्ता हुने बारम्बार वा उल्लेखनीय काल्पनिक स्थानहरूको सूची हो।
एler्गलको टेरेस: एler्गलरको टेरेसले सन्दर्भ गर्न सक्छ: सेन्काकु टापुहरू, पूर्वी चीन सागरमा विवादास्पद टापुहरू, जसलाई ताइवानमा एler्गलर टेरेस भनेर चिनिन्छ Diaoyutai राज्य गेस्टहाउस, एक ऐतिहासिक होटल र बेइजि,, चीन मा अतिथिगृह परिसर
Diaoyutai गेस्टहाउस: दियाओताई राज्य अतिथिगृह चीनको बेइजि inमा कूटनीतिक जटिल हो, जहाँ चिनियाँ राज्य नेतृत्वले विदेशी प्रतिष्ठित व्यक्तिहरूलाई स्वागत गर्न स्वागत गर्दछ। यसले विला र बगैंचाहरूको संख्या समावेश गर्दछ। होटल परिसर जम्मा दश महान भवनहरू मध्ये एकको रूपमा उल्लेख गरिएको छ, सन् १ 195 9 in मा जन गणतन्त्र चीनको १० औं वार्षिकोत्सवको लागि निर्माण गरिएको स्थलचिन्हहरूको सूची।
माछावालाको गाँठ: माछावालाको गाँठ सममितीय संरचनाको साथ झुन्डिएको छ जसमा दुई ओभरह्यान्ड गाँठाहरू हुन्छन्, प्रत्येक एक अर्कोको खण्डको वरिपरि बाँधिएको हुन्छ। मछुवाको गाँठको अन्य नामहरू: ए angle्ग्लेरसको गाँठ, अंग्रेजी गाँठ, हलिबट गाँठ, वाटरम्यानको गाँठ।
एler्गलको लुप: ए angle्गलरको लूप, अन्यथा पूर्णता लूपको रूपमा चिनिन्छ , गाँठको एक प्रकार हो जुन निश्चित लूप बनाउँदछ। राम्रो वा फिसलन रेखा को लागी उपयोगी छ, यो केहि लूप गाँठहरु मध्ये एक हो जुन बन्जी कर्डमा राम्रोसँग राख्छ। यो एकदम सुरक्षित छ, तर यो नराम्रा रूपमा जाम गर्दछ र उपयुक्त छैन यदि गाँठ खोल्न आवश्यक छ।
Angler: चेनी उपाध्यक्ष: एler्गलर: चेनी वाइस प्रेसिडेन्सी २०० 2008 मा प्रकाशित द वाशिंगटन पोस्ट अनुसन्धान रिपोर्टर बार्टन जेलमैनको पुस्तक हो। कथा वर्णन गर्दै गेलम्यानले संयुक्त राज्यका उपराष्ट्रपति डिक चेन्नेले इराकको आक्रमणको बारेमा रिपब्लिकन नेताहरुलाई इराकको खतराको बारेमा बहकाए भनेर जोड दिए। इराक संयुक्त राज्य अमेरिका द्वारा। यस पुस्तकमा चेन्ने र उनको प्रशासनको बिरूद्ध धेरै आरोपहरु छन्। पुस्तक उच्च पदका सरकारी अधिकारीहरु संग सयौं अप्रकाशित साक्षात्कार मा आधारित छ।
कमिकमा १ com 9:: हास्य मा 1989 को उल्लेखनीय घटनाहरू। हास्य मा वर्ष को सूची को भी हेर्नुहोस्।
एler्गलर (भिडियो खेल): एler्गलर एक माछा मार्ने भिडियो खेल हो जुन डर्क ओलिभियर द्वारा ZX स्पेक्ट्रमको लागि लेखिएको थियो र १ 198 33 भर्जिन गेम्स द्वारा प्रकाशित गरियो। खेलाडीले स्क्रीनको शीर्षमा डु boat्गा नियन्त्रण गर्दछ र सकेसम्म धेरै माछा समात्ने १०० वटा कस्ट्स छ।
Angler: एler्गलरले सन्दर्भ गर्न सक्दछ: ए fisher्गल गर्ने माछा मार्ने प्राविधिक प्रयोग गर्ने एक माछावाला Angler ए r्ग्r्लर , लोफियस पिस्केटरियस , एक भिक्षु सामान्यतया, कुनै पनि Angrfish क्रम लोपीफोरम एler्गलर: चेनी वाइस प्रेसिडेन्सी , २००on मा बार्टन गेलम्यानले उप-राष्ट्रपति डिक चेनीको बारेमा लेखेको पुस्तक, जसको सेक्रेट सर्भिस कोडेनेम "एler्गलर" थियो। Huawei Nexus 6P, codename कोण
Angling: एling्गलिंग एक माछा हुक वा "कोण" को माध्यमबाट माछा मार्ने तरिका हो। हुक सामान्यतया माछा मार्ने लाइनमा जोडिएको हुन्छ, जुन अक्सर माछा मार्ने डण्डमा जोडिएको हुन्छ। आधुनिक माछा मार्ने डण्डहरू सामान्यतया फिशिंग रिलले फिट हुन्छन् जुन लाइन भण्डारण, पुनःप्राप्ति र भुक्तानीको संयन्त्रको रूपमा कार्य गर्दछ। टेन्कारा फिशिंग र उखु पोल फिशिंग दुई प्रविधिहरू हुन् जसले रिल प्रयोग गर्दैन। हुक आफै चारा लगाउन सकिन्छ, तर कहिलेकाँही एकल हुक र चाराको ठाउँमा बहु जोडिएका हुकहरूको साथ प्रलोभन प्रयोग हुन्छ। एक डु indic्गा सूचक, जस्तै एक फ्लोट र तौल सिink्कर, कहिलेकाँही माछाले हुकलाई निल्यो भनेर संकेत गर्न प्रयोग गरिन्छ, जुन माछाको मुखमा ल an्गरले यसलाई छोड्ने क्रममा माछा मार्छ।
एler्गलर (भिडियो खेल): एler्गलर एक माछा मार्ने भिडियो खेल हो जुन डर्क ओलिभियर द्वारा ZX स्पेक्ट्रमको लागि लेखिएको थियो र १ 198 33 भर्जिन गेम्स द्वारा प्रकाशित गरियो। खेलाडीले स्क्रीनको शीर्षमा डु boat्गा नियन्त्रण गर्दछ र सकेसम्म धेरै माछा समात्ने १०० वटा कस्ट्स छ।
Angler POW فرار: अप्रिल १ 194 1१ मा, ताल सुपेरियरको उत्तरी किनारमा नेइस प्रान्तीय पार्क नजिकै एler्गलर POW शिविरमा रहेका कैदीहरूले दोस्रो विश्वयुद्धको बेला क्यानाडाली POW शिविरबाट सब भन्दा ठूलो भाग्ने योजना बनाए। ओन्टारियो, क्यानडामा भाग्नु आफ्नो प्रकारको सब भन्दा ठूलो थियो।
एन्जेलन काठी को Angeln Saddleback पनि एङ्गलर Sattelschwein रूपमा जानिन्छ, Schleswig-Holstein, जर्मनी मा मुख्य रूप हुर्किसकेका घरेलू सुँगुर को एक दुर्लभ नस्ल छ। यो फोरफेटमा यसको शरीरको वरिपरि सेतो बेल्टसहित ठूलो, लोप-कान भएको कालो सुँगुर हो।
चाका (माछा): Chaca को Catfish परिवार Chacidae मा मात्र जीनस छ। यी माछा सामान्यतः squarehead catfishes, frogmouth catfishes, वा Angler catfishes रूपमा परिचित छन्। यी असामान्य माछाहरूको आसीन जीवनशैली छ र उनीहरूको धेरैजसो समय गतिविहीन हुन्छ।
Anglerfish: ए r ्गलरफिश टेलिस्ट अर्डर लोपीफोर्म्सको माछा हो। तिनीहरू हड्डीको माछा हुन् जसको शिकारको तिनीहरूको चरित मोडको लागि नाम दिइएको छ, जसमा परिमार्जित लुमिनेसन्ट फिन रेले अन्य माछाको लागि प्रलोभनको रूपमा काम गर्दछ। लुमिनेसेन्स सिम्बायोटिक ब्याक्टेरियाहरूबाट आउँदछ, जुन समुद्री पानीबाट लिइएको हो भनिन्छ, जसमा एस्का र वरपर बस्ने छ।
Angling: एling्गलिंग एक माछा हुक वा "कोण" को माध्यमबाट माछा मार्ने तरिका हो। हुक सामान्यतया माछा मार्ने लाइनमा जोडिएको हुन्छ, जुन अक्सर माछा मार्ने डण्डमा जोडिएको हुन्छ। आधुनिक माछा मार्ने डण्डहरू सामान्यतया फिशिंग रिलले फिट हुन्छन् जुन लाइन भण्डारण, पुनःप्राप्ति र भुक्तानीको संयन्त्रको रूपमा कार्य गर्दछ। टेन्कारा फिशिंग र उखु पोल फिशिंग दुई प्रविधिहरू हुन् जसले रिल प्रयोग गर्दैन। हुक आफै चारा लगाउन सकिन्छ, तर कहिलेकाँही एकल हुक र चाराको ठाउँमा बहु जोडिएका हुकहरूको साथ प्रलोभन प्रयोग हुन्छ। एक डु indic्गा सूचक, जस्तै एक फ्लोट र तौल सिink्कर, कहिलेकाँही माछाले हुकलाई निल्यो भनेर संकेत गर्न प्रयोग गरिन्छ, जुन माछाको मुखमा ल an्गरले यसलाई छोड्ने क्रममा माछा मार्छ।
माछावालाको गाँठ: माछावालाको गाँठ सममितीय संरचनाको साथ झुन्डिएको छ जसमा दुई ओभरह्यान्ड गाँठाहरू हुन्छन्, प्रत्येक एक अर्कोको खण्डको वरिपरि बाँधिएको हुन्छ। मछुवाको गाँठको अन्य नामहरू: ए angle्ग्लेरसको गाँठ, अंग्रेजी गाँठ, हलिबट गाँठ, वाटरम्यानको गाँठ।