ARITH Symposium on Computer Arithmetic, ARITH Symposium on Computer Arithmetic, ARITH Symposium on Computer Arithmetic

कम्प्यूटर अंकगणितमा एरिट सिम्पोजियम: आईईईई इंटरनेशनल सिम्पोजियम ऑन कम्प्युटर अरिथेटिक ( एआरआईटीएच ) भनेको एक सम्मेलन हो कम्प्युटर अंकगणितको क्षेत्रमा। सन् १ 69। In मा यस गोष्ठी स्थापना भएको थियो, शुरूमा तीन बर्षे घटनाको रूपमा, त्यसपछि अभेद्य घटनाको रूपमा, र अन्तमा २०१ from देखि वार्षिक गोष्ठीको रूपमा।
कम्प्यूटर अंकगणितमा एरिट सिम्पोजियम: आईईईई इंटरनेशनल सिम्पोजियम ऑन कम्प्युटर अरिथेटिक ( एआरआईटीएच ) भनेको एक सम्मेलन हो कम्प्युटर अंकगणितको क्षेत्रमा। सन् १ 69। In मा यस गोष्ठी स्थापना भएको थियो, शुरूमा तीन बर्षे घटनाको रूपमा, त्यसपछि अभेद्य घटनाको रूपमा, र अन्तमा २०१ from देखि वार्षिक गोष्ठीको रूपमा।
कम्प्यूटर अंकगणितमा एरिट सिम्पोजियम: आईईईई इंटरनेशनल सिम्पोजियम ऑन कम्प्युटर अरिथेटिक ( एआरआईटीएच ) भनेको एक सम्मेलन हो कम्प्युटर अंकगणितको क्षेत्रमा। सन् १ 69। In मा यस गोष्ठी स्थापना भएको थियो, शुरूमा तीन बर्षे घटनाको रूपमा, त्यसपछि अभेद्य घटनाको रूपमा, र अन्तमा २०१ from देखि वार्षिक गोष्ठीको रूपमा।
कम्प्यूटर अंकगणितमा एरिट सिम्पोजियम: आईईईई इंटरनेशनल सिम्पोजियम ऑन कम्प्युटर अरिथेटिक ( एआरआईटीएच ) भनेको एक सम्मेलन हो कम्प्युटर अंकगणितको क्षेत्रमा। सन् १ 69। In मा यस गोष्ठी स्थापना भएको थियो, शुरूमा तीन बर्षे घटनाको रूपमा, त्यसपछि अभेद्य घटनाको रूपमा, र अन्तमा २०१ from देखि वार्षिक गोष्ठीको रूपमा।
कम्प्यूटर अंकगणितमा एरिट सिम्पोजियम: आईईईई इंटरनेशनल सिम्पोजियम ऑन कम्प्युटर अरिथेटिक ( एआरआईटीएच ) भनेको एक सम्मेलन हो कम्प्युटर अंकगणितको क्षेत्रमा। सन् १ 69। In मा यस गोष्ठी स्थापना भएको थियो, शुरूमा तीन बर्षे घटनाको रूपमा, त्यसपछि अभेद्य घटनाको रूपमा, र अन्तमा २०१ from देखि वार्षिक गोष्ठीको रूपमा।
अरिथ भान हर्क: अरिथ भान हर्क ,, क्यानाडाली लेखक, आलोचक, सम्पादक, सार्वजनिक बौद्धिक, र विश्वविद्यालय प्राध्यापक हुन्। उनको काममा अक्सर नारीवादी थिमहरू समावेश हुन्छन्, र पश्चिमी क्यानाडाको संस्कृति चित्रण र विश्लेषण गर्दछ।
अरिथ भान हर्क: अरिथ भान हर्क ,, क्यानाडाली लेखक, आलोचक, सम्पादक, सार्वजनिक बौद्धिक, र विश्वविद्यालय प्राध्यापक हुन्। उनको काममा अक्सर नारीवादी थिमहरू समावेश हुन्छन्, र पश्चिमी क्यानाडाको संस्कृति चित्रण र विश्लेषण गर्दछ।
अरिथांग (विधान सभा क्षेत्र): अरिथांग भारतको उत्तर पूर्वी राज्य सिक्किमको assembly२ वटा विधानसभा क्षेत्र मध्ये एक हो। यो क्षेत्र सिक्किम लोकसभा क्षेत्र अन्तर्गत पर्दछ।
अंकगणित: आधुनिक संख्यावाचक शब्दावलीमा, अंकगणित भनेको कुनै शब्द वा वाक्यांशलाई संख्यात्मक मान प्रदान गर्ने आधारमा भविष्यवाणीको एक रूप हो जुन पुरानो ग्रीक आइसोप्सी वा हिब्रू / अरमाईक गेमेट्रियाको सरलीकृत संस्करणको रूपमा ल्याटिन वर्णमालामा अनुकूल छ। अरिथमान्सी कल्दीहरू, प्लेटोनिस्टहरू, पायथागोरियन्स र काबालाहसँग सम्बन्धित छ। जब कौशलता एक व्यक्तिको नाममा लागू हुन्छ, यो ओमान्मेन्सीको एक रूप हो।
अरिथमोमानिया: अरिथमोमानिया एक मानसिक विकार हो जुन जुन जुनै जुनूनदार – बाध्यकारी विकार (ओसीडी) को अभिव्यक्तिको रूपमा देख्न सकिन्छ। यस विकारबाट पीडित व्यक्तिहरूको आफ्नो कार्यहरू वा वस्तुहरू वरपरका ठाउँहरूमा गणना गर्न दृढ आवश्यकता छ।
अंकगणित: आधुनिक संख्यावाचक शब्दावलीमा, अंकगणित भनेको कुनै शब्द वा वाक्यांशलाई संख्यात्मक मान प्रदान गर्ने आधारमा भविष्यवाणीको एक रूप हो जुन पुरानो ग्रीक आइसोप्सी वा हिब्रू / अरमाईक गेमेट्रियाको सरलीकृत संस्करणको रूपमा ल्याटिन वर्णमालामा अनुकूल छ। अरिथमान्सी कल्दीहरू, प्लेटोनिस्टहरू, पायथागोरियन्स र काबालाहसँग सम्बन्धित छ। जब कौशलता एक व्यक्तिको नाममा लागू हुन्छ, यो ओमान्मेन्सीको एक रूप हो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
एल्गोरिदम ट्रेडिंग: एल्गोरिदम ट्रेडिंग अर्डरहरू कार्यान्वयन गर्ने एक विधि हो जुन स्वचालित पूर्व-प्रोग्रामेड ट्रेडिंग निर्देशहरू हिसाबले समय, मूल्य, र भोल्युमको लागि लेखांकनको प्रयोग गरेर हुन्छ। यस प्रकारको ट्रेडिंगले मानव व्यापारीहरूसँग सम्बन्धित कम्प्युटरहरूको गती र कम्प्यूटेशनल संसाधनहरूको लाभ उठाउन प्रयास गर्दछ। एक्काईसौं शताब्दीमा, एल्गोरिथमिक ट्रेडिंग दुबै खुद्रा र संस्थागत ट्रेडरहरूसँग क्रेसन हुँदै आएको छ। यो व्यापक रूपमा लगानी बैंकहरू, पेन्सन कोष, म्युचुअल फन्डहरू, र हेज कोषहरू द्वारा प्रयोग गरिन्छ जुन ठूलो अर्डरको कार्यान्वयन फैलाउन वा मानव व्यापारिकहरूलाई प्रतिक्रिया दिनको लागि धेरै छिटो कारोबार गर्न आवश्यक पर्दछ। २०१ 2019 मा गरिएको एक अध्ययनले देखायो कि विदेशी मुद्रा बजारमा करिब 92 २% ट्रेडिंग मानव भन्दा एल्गोरिदम ट्रेडिंगद्वारा गरिएको थियो।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको साधारण फरकको साथ अंकगणितको प्रगति हो।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको साधारण फरकको साथ अंकगणितको प्रगति हो।
अरिथमौरल: अरिथमेरेल एक मेकानिकल क्यालकुलेटर थियो कि एक धेरै सहज उपयोगकर्ता ईन्टरफेस थियो, खास गरी गुणा गर्न र संख्या विभाजन गर्नका लागि परिणाम देखा पर्‍यो ओपेरेन्डहरू प्रविष्ट हुने बित्तिकै। यो पहिलो पटक फ्रान्समा १ Tim42२ मा टिमोलियन मउरेलले पेटन्ट गरेका थिए। यसले १ 18 national in मा फ्रान्सको फ्रान्सेली राष्ट्रिय कार्यक्रममा स्वर्ण पदक प्राप्त गर्‍यो। दुर्भाग्यवश यसको जटिलता र यसको डिजाइनको कमजोरपनले यसलाई निर्माण हुनबाट रोकेको थियो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित – ज्यामितीय मतलब: गणितमा, अंकगणित – ज्यामितीय माने दुई सकारात्मक वास्तविक संख्या x र y परिभाषित गरिएको छ:
अंकगणित र ज्यामितीय साधनको असमानता: गणितमा, अंकगणित र ज्यामितीय साधनको असमानता , वा अधिक संक्षेपमा एएम – जीएम असमानता , बताउँछ कि गैर-नकारात्मक वास्तविक संख्याहरूको सूचीको अंकगणित माध्य एउटै सूचीको ज्यामितीय मतलब भन्दा ठूलो वा बराबर हो; र अगाडि, ती दुई साधनहरू बराबर छन् र मात्र यदि सूचीमा प्रत्येक संख्या समान छ।
अंकगणित – ज्यामितीय मतलब: गणितमा, अंकगणित – ज्यामितीय माने दुई सकारात्मक वास्तविक संख्या x र y परिभाषित गरिएको छ:
ज्यामितीय मतलब: गणितमा, ज्यामितीय माध्य एक माध्य या औसत हो, जसले केन्द्रीय प्रवृत्ति वा संख्याको सेटको विशिष्ट मानलाई तिनीहरूको मानहरूको उत्पादन प्रयोग गरेर संकेत गर्दछ। Geometric माध्य संख्या 1 एक्स को एक सेट को लागि, N संख्या, अर्थात् को उत्पादन को N औं मूल रूपमा परिभाषित गरिएको छ, एक्स 2, ..., N, geometric माध्य रूपमा परिभाषित गरिएको छ x
लोगारिथमिक मतलब: गणितमा, लोगारिदम मतलब भनेको दुई गैर negativeणात्मक नम्बरहरूको प्रकार्य हो जुन उनीहरूको भिन्नताको बराबर हो जुन उनीहरूको भागफलको लघुगणकले विभाजित गर्दछ। यो गणना गर्मी र सामूहिक ट्रान्सफर समावेश ईन्जिनियरिंग समस्याहरूमा लागू हुन्छ।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित (गीत): " अंकगणित " २०० Bro मा रिलीज गरिएको ब्रूक फ्रेजर द्वारा एकल हो। गीत फ्रेजरको पहिलो एल्बम के गर्ने हो कि डेलाइटको साथ पहिलो ट्र्याक हो। यो गीत पछि सोनी बीएमजी कम्प्लेसन मोर नेचरमा समावेश गरिएको थियो, न्युजील्याण्ड सोनी बीएमजी क्याटलगबाट गीतहरूको संग्रह।
अंकगणित (गीत): " अंकगणित " २०० Bro मा रिलीज गरिएको ब्रूक फ्रेजर द्वारा एकल हो। गीत फ्रेजरको पहिलो एल्बम के गर्ने हो कि डेलाइटको साथ पहिलो ट्र्याक हो। यो गीत पछि सोनी बीएमजी कम्प्लेसन मोर नेचरमा समावेश गरिएको थियो, न्युजील्याण्ड सोनी बीएमजी क्याटलगबाट गीतहरूको संग्रह।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित ज्यामिति: गणितमा, अंकगणित ज्यामिति लगभग बीजगणित ज्यामिति देखि संख्या सिद्धान्त मा समस्या गर्न प्रविधिको उपयोग हो। अंकगणित ज्यामिति डायफान्टिन ज्यामितीयको वरिपरि केन्द्रित हुन्छ, बीजगणित प्रजातिहरूका तर्कसंगत बिन्दुहरूको अध्ययन।
अराकेलोभ सिद्धान्त: गणितमा, अरकेलोभ सिद्धान्त डायओफान्टिन ज्यामितिमा एक दृष्टिकोण हो, सुरेन अरकेलोभको लागि नामकरण गरिएको। यो उच्च आयाममा डियोफ्यान्टाइन समीकरणहरूको अध्ययन गर्न प्रयोग गरिन्छ।
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अंकगणित र ज्यामितीय Frobenius: गणितमा, फ्रोबिनियस एन्डोमोर्फिजम कुनै पनि कम्युटेटिभ रिंग आरमा परिभाषित गरिएको हुन्छ जसको विशेषता p , जहाँ p प्राथमिक संख्या हो। अर्थात्, आर पी गर्न आर मा आर लिन्छ कि म्यापिङ φ आर को घन्टी endomorphism छ।
फ्रोबेनियस एंडोमोर्फिजम: कम्युटेटिभ बीजगणित र क्षेत्र सिद्धान्तमा, फ्र्रोबिनियस एंडोमोर्फिजम कम्युटिभ रिंगको विशेष एंडोमोर्फिजम हो प्राइम चारित्रिक पी , एक महत्त्वपूर्ण वर्ग जसमा सीमित क्षेत्रहरू समावेश छन्। एन्डोमोर्फिजमले प्रत्येक तत्वलाई यसको p -th पावरमा म्याप गर्दछ। केही सन्दर्भहरूमा यो एक अटोमोर्फिजम हो, तर यो सामान्यमा सत्य हुँदैन।
अंकगणित Fuchsian समूह: अंकगणित फुचियन समूह फुचियन समूहहरूको विशेष वर्ग हो जुन क्वाटरियन बीजगणितहरूमा अर्डरको प्रयोग गरेर निर्माण गरियो। तिनीहरू अंकगणित समूहहरूका विशेष उदाहरणहरू हुन्। अंकगणित Fuchsian समूह को प्रोटोटाइपिकल उदाहरण मोड्युलर समूह हो । तिनीहरू, र हाइपरबोलिक सतहले तिनीहरूको हाइपरबोलिक प्लेनमा तिनीहरूको कार्यसँग सम्बन्धित प्रायः फुसियन समूहहरू र हाइपरबोलिक सतहहरू बीच नियमित व्यवहार प्रदर्शन गर्दछ।
अंकगणित ज्यामिति: गणितमा, अंकगणित ज्यामिति लगभग बीजगणित ज्यामिति देखि संख्या सिद्धान्त मा समस्या गर्न प्रविधिको उपयोग हो। अंकगणित ज्यामिति डायफान्टिन ज्यामितीयको वरिपरि केन्द्रित हुन्छ, बीजगणित प्रजातिहरूका तर्कसंगत बिन्दुहरूको अध्ययन।
अंकगणित IF: अंकगणित IF कथन एक तीन तरणित अंकगणित कन्डिसन कथन हो, जुन १ 195 7 in मा फोर्ट्रानको पहिलो विमोचनमा पहिलो पटक देखीएको थियो, र पछि सबै संस्करणहरूमा फेला पर्‍यो, र केही अन्य प्रोग्रामिंग भाषाहरू, जस्तै FOCAL। तार्किक IF कथन अन्य भाषाहरूमा देखीएको विपरीत, फोर्ट्रान स्टेटमेन्टले तीन फरक शाखालाई परिभाषित गर्छ कि एक अभिव्यक्तिको नतीजा नकारात्मक, शून्य, वा सकारात्मक छ भने, क्रम अनुसार:
अंकगणित हाइपरबोलिक--मनिफोल्ड: गणितमा, स्पष्ट रूपमा समूह सिद्धान्त र हाइपरबोलिक ज्यामितिमा, अंकगणित क्लेनियन समूह क्लेटरियन समूहहरूको विशेष वर्ग हुन् जुन क्वाटरियन बीजगणितमा आदेश प्रयोग गरेर निर्माण गरिएको थियो। तिनीहरू अंकगणित समूहहरूका विशेष उदाहरणहरू हुन्। एक अंकगणित हाइपरबोलिक तीन-मनिफोल्ड हाइपरबोलिक स्पेसको भागफल हो एक अंकगणित क्लेनियन समूह द्वारा। यी मनिफोल्डहरूले केही विशेष रूपमा सुन्दर वा उल्लेखनीय उदाहरणहरू समावेश गर्दछ।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित माध्य: गणित र तथ्या .्कमा , अंकगणित माध्य , वा साधारण माध्य वा औसत , स numbers्ग्रहमा संख्याहरूको गणना द्वारा विभाजित संख्याको संग्रहको योग हो। संग्रह प्राय: प्रयोगको परीक्षण वा अवलोकनात्मक अध्ययनको नतीजाको सेट हो, वा प्रायः सर्वेक्षणहरूबाट परिणामहरूको सेट हुन्छ। गणित र तथ्या .्कको केही प्रस in्गमा "अंकगणित मीन" भन्ने शव्दलाई प्राथमिकता दिइन्छ, किनकि यसले ज्यामितीय माध्य र हार्मोनिक मध्य जस्ता अन्य माध्यमहरू भन्दा यसलाई छुट्याउन मद्दत गर्दछ।
अंकगणित र ज्यामितीय साधनको असमानता: गणितमा, अंकगणित र ज्यामितीय साधनको असमानता , वा अधिक संक्षेपमा एएम – जीएम असमानता , बताउँछ कि गैर-नकारात्मक वास्तविक संख्याहरूको सूचीको अंकगणित माध्य एउटै सूचीको ज्यामितीय मतलब भन्दा ठूलो वा बराबर हो; र अगाडि, ती दुई साधनहरू बराबर छन् र मात्र यदि सूचीमा प्रत्येक संख्या समान छ।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको साधारण फरकको साथ अंकगणितको प्रगति हो।
अराकेलोभ सिद्धान्त: गणितमा, अरकेलोभ सिद्धान्त डायओफान्टिन ज्यामितिमा एक दृष्टिकोण हो, सुरेन अरकेलोभको लागि नामकरण गरिएको। यो उच्च आयाममा डियोफ्यान्टाइन समीकरणहरूको अध्ययन गर्न प्रयोग गरिन्छ।
अराकेलोभ सिद्धान्त: गणितमा, अरकेलोभ सिद्धान्त डायओफान्टिन ज्यामितिमा एक दृष्टिकोण हो, सुरेन अरकेलोभको लागि नामकरण गरिएको। यो उच्च आयाममा डियोफ्यान्टाइन समीकरणहरूको अध्ययन गर्न प्रयोग गरिन्छ।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको साधारण फरकको साथ अंकगणितको प्रगति हो।
अंकगणित सतह: गणितमा, फ्रडेक्स क्षेत्रको साथ डेडेकिन्ड डोमेन आर माथि अंकगणित सतह एक ज्यामितीय वस्तु एक पारंपरिक आयाम, र एक अन्य आयाम प्राइमन्स को असीमित द्वारा प्रदान गरीएको हो। आर पूर्णाङ्कहरुको Z को घन्टी छ, यो अंतर्ज्ञान प्रमुख आदर्श स्पेक्ट्रम युक्ति (Z) मा निर्भर गर्दछ एक लाइन analogous रूपमा देखेको भइरहेको। अंकगणित सतहहरू डायफान्टिन ज्यामितिमा स्वाभाविक रूपमा देखा पर्दछ, जब K लाई परिभाषित एक बीजगणित कर्भ क्षेत्र R / P मा घटाइएको छ भन्ने सोच्दछ, जहाँ P सबै भन्दा P को R को एक आदर्श आदर्श हो; र R / P लाई घटाउने प्रक्रियाको बारेमा के हुन्छ भनेर निर्दिष्ट गर्न मद्दत पुर्‍याउँछ जब सबै भन्दा भोला बाटोले अर्थ प्राप्त गर्न असफल हुन्छ।
एल्गोरिदम ट्रेडिंग: एल्गोरिदम ट्रेडिंग अर्डरहरू कार्यान्वयन गर्ने एक विधि हो जुन स्वचालित पूर्व-प्रोग्रामेड ट्रेडिंग निर्देशहरू हिसाबले समय, मूल्य, र भोल्युमको लागि लेखांकनको प्रयोग गरेर हुन्छ। यस प्रकारको ट्रेडिंगले मानव व्यापारीहरूसँग सम्बन्धित कम्प्युटरहरूको गती र कम्प्यूटेशनल संसाधनहरूको लाभ उठाउन प्रयास गर्दछ। एक्काईसौं शताब्दीमा, एल्गोरिथमिक ट्रेडिंग दुबै खुद्रा र संस्थागत ट्रेडरहरूसँग क्रेसन हुँदै आएको छ। यो व्यापक रूपमा लगानी बैंकहरू, पेन्सन कोष, म्युचुअल फन्डहरू, र हेज कोषहरू द्वारा प्रयोग गरिन्छ जुन ठूलो अर्डरको कार्यान्वयन फैलाउन वा मानव व्यापारिकहरूलाई प्रतिक्रिया दिनको लागि धेरै छिटो कारोबार गर्न आवश्यक पर्दछ। २०१ 2019 मा गरिएको एक अध्ययनले देखायो कि विदेशी मुद्रा बजारमा करिब 92 २% ट्रेडिंग मानव भन्दा एल्गोरिदम ट्रेडिंगद्वारा गरिएको थियो।
अंकगणित ज्यामिति: गणितमा, अंकगणित ज्यामिति लगभग बीजगणित ज्यामिति देखि संख्या सिद्धान्त मा समस्या गर्न प्रविधिको उपयोग हो। अंकगणित ज्यामिति डायफान्टिन ज्यामितीयको वरिपरि केन्द्रित हुन्छ, बीजगणित प्रजातिहरूका तर्कसंगत बिन्दुहरूको अध्ययन।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित र ज्यामितीय Frobenius: गणितमा, फ्रोबिनियस एन्डोमोर्फिजम कुनै पनि कम्युटेटिभ रिंग आरमा परिभाषित गरिएको हुन्छ जसको विशेषता p , जहाँ p प्राथमिक संख्या हो। अर्थात्, आर पी गर्न आर मा आर लिन्छ कि म्यापिङ φ आर को घन्टी endomorphism छ।
अंकगणित र ज्यामितीय Frobenius: गणितमा, फ्रोबिनियस एन्डोमोर्फिजम कुनै पनि कम्युटेटिभ रिंग आरमा परिभाषित गरिएको हुन्छ जसको विशेषता p , जहाँ p प्राथमिक संख्या हो। अर्थात्, आर पी गर्न आर मा आर लिन्छ कि म्यापिङ φ आर को घन्टी endomorphism छ।
निर्देशन सेट आर्किटेक्चर: कम्प्युटर विज्ञानमा, एक निर्देश सेट आर्किटेक्चर ( ISA ) कम्प्यूटरको एक अमूर्त मोडेल हो। यसलाई आर्किटेक्चर वा कम्प्यूटर आर्किटेक्चरको रूपमा पनि चिनिन्छ। एक ISA को अनुभूति, जस्तै केन्द्रीय प्रशोधन एकाई (CPU), एक कार्यान्वयन भनिन्छ।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
औसत: बोलचालको भाषामा, औसत एकल संख्या हो जसमा खाली स्थान संख्याको प्रतिनिधित्व गर्दछ। औसतका विभिन्न अवधारणाहरू विभिन्न प्रस in्गहरूमा प्रयोग गरिन्छ। अक्सर "औसत" ले अंकगणितको अर्थ बुझाउँदछ, संख्याहरूको योग कति संख्याको आधारमा विभाजित हुन्छ औसत। तथ्या .्कहरूमा, मध्य, मध्य र मोड सबै केन्द्रीय प्रवृत्तिको उपायको रूपमा चिनिन्छ, र बोलचाल प्रयोगमा यी कुनै पनिलाई औसत मान भन्न सकिन्छ।
अंकगणित बिलियर्ड्स: मनोरञ्जनात्मक गणितमा, अंकगणित बिलियर्ड्स एक ज्यामितीय विधि प्रदान गर्दछ कम से कम साधारण बहुलाई र दुई प्राकृतिक संख्याहरूको सबैभन्दा ठूलो साधारण विभाजक आयत भित्र प्रतिबिम्ब को उपयोग गरेर जसको पक्षहरू दुई दिइएका संख्या हुन्। यो गतिशील बिलियर्ड्सको ट्र्याजेक्टरी विश्लेषणको सजिलो उदाहरण हो।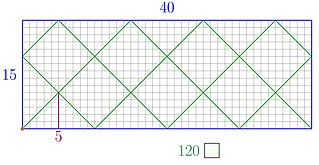
अंकगणित सर्किट जटिलता: कम्प्यूटेशनल जटिलता सिद्धान्तमा, अंकगणित सर्किट बहु गणितहरू गणना गर्ने मानक मोडल हुन्। अनौपचारिक रूपमा, अंकगणित सर्किटले इनपुट गर्दछ कि त भ्यारीएबल वा नम्बरहरू लिन्छ, र कि त यो पहिले नै गणना गरिएको दुई अभिव्यक्तिहरू थप्न वा गुणा गर्न अनुमति छ। अंकगणित सर्किटहरूले बहुगणनाहरू गणना गर्ने जटिलता बुझ्ने औपचारिक तरीका प्रदान गर्दछ। अनुसन्धानको यस प in्क्तिमा आधारभूत प्रकारको प्रश्न "दिइएको बहुपद गणना गर्ने सबैभन्दा प्रभावकारी तरिका के हो "?
अंकगणित सर्किट जटिलता: कम्प्यूटेशनल जटिलता सिद्धान्तमा, अंकगणित सर्किट बहु गणितहरू गणना गर्ने मानक मोडल हुन्। अनौपचारिक रूपमा, अंकगणित सर्किटले इनपुट गर्दछ कि त भ्यारीएबल वा नम्बरहरू लिन्छ, र कि त यो पहिले नै गणना गरिएको दुई अभिव्यक्तिहरू थप्न वा गुणा गर्न अनुमति छ। अंकगणित सर्किटहरूले बहुगणनाहरू गणना गर्ने जटिलता बुझ्ने औपचारिक तरीका प्रदान गर्दछ। अनुसन्धानको यस प in्क्तिमा आधारभूत प्रकारको प्रश्न "दिइएको बहुपद गणना गर्ने सबैभन्दा प्रभावकारी तरिका के हो "?
अंकगणित सर्किट जटिलता: कम्प्यूटेशनल जटिलता सिद्धान्तमा, अंकगणित सर्किट बहु गणितहरू गणना गर्ने मानक मोडल हुन्। अनौपचारिक रूपमा, अंकगणित सर्किटले इनपुट गर्दछ कि त भ्यारीएबल वा नम्बरहरू लिन्छ, र कि त यो पहिले नै गणना गरिएको दुई अभिव्यक्तिहरू थप्न वा गुणा गर्न अनुमति छ। अंकगणित सर्किटहरूले बहुगणनाहरू गणना गर्ने जटिलता बुझ्ने औपचारिक तरीका प्रदान गर्दछ। अनुसन्धानको यस प in्क्तिमा आधारभूत प्रकारको प्रश्न "दिइएको बहुपद गणना गर्ने सबैभन्दा प्रभावकारी तरिका के हो "?
अंकगणित सर्किट जटिलता: कम्प्यूटेशनल जटिलता सिद्धान्तमा, अंकगणित सर्किट बहु गणितहरू गणना गर्ने मानक मोडल हुन्। अनौपचारिक रूपमा, अंकगणित सर्किटले इनपुट गर्दछ कि त भ्यारीएबल वा नम्बरहरू लिन्छ, र कि त यो पहिले नै गणना गरिएको दुई अभिव्यक्तिहरू थप्न वा गुणा गर्न अनुमति छ। अंकगणित सर्किटहरूले बहुगणनाहरू गणना गर्ने जटिलता बुझ्ने औपचारिक तरीका प्रदान गर्दछ। अनुसन्धानको यस प in्क्तिमा आधारभूत प्रकारको प्रश्न "दिइएको बहुपद गणना गर्ने सबैभन्दा प्रभावकारी तरिका के हो "?
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अंकगणित संयोजन: गणितमा, अंकगणित कम्बिनेटरिक्स संख्या सिद्धान्त, कम्बिनेटोरिक्स, एर्गोडिक थ्योरी र हर्मोनिक विश्लेषणको छेउछाउको क्षेत्र हो।
द्रुत फुरियर रूपान्तरण: एक फास्ट फुरियर ट्रान्सफॉर्म ( FFT ) एक एल्गोरिथ्म हो कि एक अनुक्रमको असतत फुरियर रूपान्तरण (DFT), वा यसको व्युत्क्रम (IDFT) गणना गर्दछ। फुरियर विश्लेषणले यसको मूल डोमेनबाट फ्रिक्वेन्सी डोमेनमा प्रतिनिधित्वमा बदल्छ र यसको विपरित गर्दछ। DFT विभिन्न आवृत्तियों को अवयवहरूमा मानहरूको अनुक्रम विघटन गरेर प्राप्त गरिन्छ। यो अपरेशन धेरै क्षेत्रमा उपयोगी छ, तर यसलाई परिभाषाबाट सि comp्गो गणना गर्नु व्यावहारिक हुन प्राय ढिलो हुन्छ। एक FFT छिटो DFT म्याट्रिक्सलाई स्पार्स कारकको उत्पादनमा कारक गरेर त्यस्ता परिवर्तनहरूको गणना गर्दछ। नतिजाको रूपमा, यसले DFT कम्प्युटि ofको जटिलता कम गर्नका लागि प्रबन्ध गर्दछ , उठ्छ यदि एक मात्र DFT को परिभाषा लागू, गर्न को लागी , जहाँ डाटा आकार हो। गतिमा भिन्नता ठूलो हुन सक्छ, विशेष गरी लामो डाटा सेटहरूको लागि जहाँ N हजारौं वा लाखौंमा हुन सक्छ। राउन्ड-अफ त्रुटिको उपस्थितिमा धेरै एफएफटी एल्गोरिदमहरू प्रत्यक्ष वा अप्रत्यक्ष रूपमा DFT परिभाषाको मूल्या than्कन भन्दा धेरै सही हुन्छन्। त्यहाँ धेरै भिन्न FFT एल्गोरिदमहरू प्रकाशित सिद्धान्तहरूको विस्तृत श्रृंखलामा आधारित छन्, सरल जटिल संख्या अंकगणितदेखि समूह सिद्धान्त र संख्या सिद्धान्त।
द्रुत फुरियर रूपान्तरण: एक फास्ट फुरियर ट्रान्सफॉर्म ( FFT ) एक एल्गोरिथ्म हो कि एक अनुक्रमको असतत फुरियर रूपान्तरण (DFT), वा यसको व्युत्क्रम (IDFT) गणना गर्दछ। फुरियर विश्लेषणले यसको मूल डोमेनबाट फ्रिक्वेन्सी डोमेनमा प्रतिनिधित्वमा बदल्छ र यसको विपरित गर्दछ। DFT विभिन्न आवृत्तियों को अवयवहरूमा मानहरूको अनुक्रम विघटन गरेर प्राप्त गरिन्छ। यो अपरेशन धेरै क्षेत्रमा उपयोगी छ, तर यसलाई परिभाषाबाट सि comp्गो गणना गर्नु व्यावहारिक हुन प्राय ढिलो हुन्छ। एक FFT छिटो DFT म्याट्रिक्सलाई स्पार्स कारकको उत्पादनमा कारक गरेर त्यस्ता परिवर्तनहरूको गणना गर्दछ। नतिजाको रूपमा, यसले DFT कम्प्युटि ofको जटिलता कम गर्नका लागि प्रबन्ध गर्दछ , उठ्छ यदि एक मात्र DFT को परिभाषा लागू, गर्न को लागी , जहाँ डाटा आकार हो। गतिमा भिन्नता ठूलो हुन सक्छ, विशेष गरी लामो डाटा सेटहरूको लागि जहाँ N हजारौं वा लाखौंमा हुन सक्छ। राउन्ड-अफ त्रुटिको उपस्थितिमा धेरै एफएफटी एल्गोरिदमहरू प्रत्यक्ष वा अप्रत्यक्ष रूपमा DFT परिभाषाको मूल्या than्कन भन्दा धेरै सही हुन्छन्। त्यहाँ धेरै भिन्न FFT एल्गोरिदमहरू प्रकाशित सिद्धान्तहरूको विस्तृत श्रृंखलामा आधारित छन्, सरल जटिल संख्या अंकगणितदेखि समूह सिद्धान्त र संख्या सिद्धान्त।
अन्तर्-सार्वभौमिक Teichmüller सिद्धान्त: अन्तर विश्वव्यापी टेचमल्लर सिद्धान्तलाई गणितज्ञ शिनिची मोचीजुकीले २००० को दशकमा विकसित गरेको एउटा सिद्धान्तलाई त्यो नाम दिए जुन उनले अंकगणित ज्यामितिमा पहिले काम गरेको थियो। मोचीजुकीका अनुसार यो "अण्डाकार वक्रले सुसज्जित संख्या फिल्डका लागि टेचमल्लर सिद्धान्तको अंकगणित संस्करण हो"। यो सिद्धान्त २०१२ मा प्रकाशित गरिएको चार प्रिप्रिन्टहरूको श्रृंखलामा सार्वजनिक गरियो। सिद्धान्तको सब भन्दा उल्लेखनीय दावी एप्लिकेसन भनेको नम्बर थ्योरीमा विभिन्न उल्लेखनीय अनुमानहरू, विशेष गरी एबीसी अनुमानको लागि एक प्रमाण प्रदान गर्नु हो। मोचीजुकी र केही अन्य गणितज्ञहरू भन्छन् कि सिद्धान्तले वास्तवमै त्यस्तो प्रमाण दिन्छ तर यो गणितिय समुदायले अहिलेसम्म स्वीकार गरेको छैन।
प्राकृतिक घनत्व: संख्या सिद्धान्तमा, प्राकृतिक घनत्व प्राकृतिक विधिहरूको सेटको उपसेट कति "ठूलो" हुन्छ भनेर मापन गर्ने एक विधि हो। यो मुख्यतया चाहिएको सबसेटको सदस्यहरूको सामना गर्ने सम्भावनामा निर्भर गर्दछ जब अन्तराल [१, n ] मार्फत एन ठूलो हुँदै जान्छ।
अंकगणित व्युत्पन्न: संख्या सिद्धान्तमा, लगारियस अंकगणित व्युत्पन्न , वा संख्या डेरिभेटिभ , गणित विश्लेषणको लागि प्रयोग गरिएको फंक्शनको व्युत्पन्नका लागि उत्पाद नियमसँग समानता द्वारा मूल कारककरणको आधारमा पूर्णांकको लागि परिभाषित कार्य हो।
अंकगणित गतिशीलता: अंकगणित गतिशीलता एक क्षेत्र हो जुन गणित, गतिशील प्रणाली र संख्या सिद्धान्तको दुई क्षेत्रहरूलाई मिल्दछ। शास्त्रीय रूपमा, असतुल्य गतिशीलता जटिल प्लेन वा वास्तविक रेखाको सेल्फ नक्शाको पुनरावृत्तिको अध्ययनलाई जनाउँछ। अंकगणित गतिशीलता बहु-वा तर्कसंगत प्रकार्यको बारम्बार आवेदन अन्तर्गत पूर्णांक, तर्कसंगत, p -adic, र / वा बीजगणित बिन्दुहरूको संख्या-सैद्धांतिक गुणहरूको अध्ययन हो। एक आधारभूत लक्ष्य अन्तर्निहित ज्यामितीय संरचनाको मामलामा अंकगणित गुणहरू वर्णन गर्नु हो।
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अंकगणित कोड: अंकगणित कोडिंग ( AC ) एन्ट्रोपी स enc्केतनको एक रूप हो जसमा डाटा रहित डाटा सression्कुचनमा प्रयोग हुन्छ। सामान्यतया, क्यारेक्टरको स्ट्रि शब्दहरू "नमस्कार त्यहाँ" ASCII कोडमा प्रति अक्षर बिट्सको निश्चित संख्या प्रयोग गरेर प्रस्तुत गरिन्छ। जब स्ट्रि arगलाई अंकगणितको सod्केतनमा रूपान्तरण गरिन्छ, प्राय: प्रयोग हुने क्यारेक्टरहरू थोरै बिट्समा भण्डार हुनेछन् र त्यसो भएन-प्रायः हुने वर्णहरू अधिक बिटको साथ भण्डार हुनेछन्, परिणामस्वरूप कम बिट्समा कुल प्रयोग हुन्छ। अंकगणित कोडिंग एन्ट्रोपी सod्केतनको अन्य रूपहरू भन्दा भिन्न हुन्छन्, जस्तै हफम्यान कोडि component, त्यसमा इनपुटलाई कम्पोनेन्ट प्रतीकहरूमा विभाजन गर्नु र प्रत्येकलाई कोडको साथ बदल्नु भन्दा पनि अंकगणित कोडनले सम्पूर्ण सन्देशलाई एकल संख्यामा इन्कोड गर्दछ, एक अनियंत्रित-परिशुद्धता अंश क्यू , जहाँ ०.० ≤ क्यू <१.० यो वर्तमान संख्याको दायराको रूपमा प्रतिनिधित्व गर्दछ, दुई संख्याले परिभाषित गर्दछ। एन्ट्रोपी कोडरहरूको भर्खरको परिवारले असममित संख्यात्मक प्रणालीहरू छिटो कार्यान्वयनको लागि अनुमति दिन्छ हालको जानकारीको प्रतिनिधित्व गर्ने एकल प्राकृतिक संख्यामा सीधा अपरेट गर्नका लागि।
अभिव्यक्ति (गणित): गणितमा, अभिव्यक्ति वा गणितीय अभिव्यक्ति प्रतीकहरूको एक सीमित संयोजन हो जुन प्रस on्गमा निर्भर नियमहरू अनुसार राम्ररी गठन हुन्छ। गणितीय प्रतीकले अपरेसनहरूको अर्डर निर्धारण गर्न मद्दतको लागि संख्याहरू (स्थिरताहरू), चरहरू, अपरेसनहरू, प्रकारहरू, कोष्ठक, विराम चिह्न र समूहबद्ध गर्न सक्दछ, र तार्किक सिन्ट्याक्सको अन्य पक्षहरू।
अभिभावकहरूको लागि अंकगणित: अंकगणितका लागि अभिभावक गणित शिक्षाको बारेमा पुस्तक आमा बुबा र शिक्षकहरूको उद्देश्य हो।
अभिभावकहरूको लागि अंकगणित: अंकगणितका लागि अभिभावक गणित शिक्षाको बारेमा पुस्तक आमा बुबा र शिक्षकहरूको उद्देश्य हो।
पेनो अक्षहरू: गणितीय तर्कमा, पेनाओ अक्षहरू , जसलाई डेडेकिन्ड – पियानो अक्सिओम वा पियानो पोस्ट्युलेटहरू पनि भनिन्छ, १ th औं शताब्दीका इतालवी गणितज्ञ ज्युसेप्पे पानाले प्रस्तुत गरेका प्राकृतिक संख्याका लागि अक्सिओमहरू हुन्। यी axioms संख्या सिद्धांत संगत र पूर्ण छ कि छैन भन्ने आधारभूत प्रश्नहरूमा अनुसन्धान सहित, धेरै metamathematical अनुसन्धान मा लगभग अपरिवर्तित प्रयोग भएको छ।
अंश: भिन्न अंशले पूरैको अंश प्रतिनिधित्व गर्दछ, अधिक सामान्यतया, समान भागहरूको संख्या। जब दैनिक अंग्रेजीमा बोल्छ, एक अंशले निर्दिष्ट आकारको कति भागहरू हुन्छन् उदाहरणका लागि, एक-आधा, आठ-पचासौं, तीन-चतुर्थांश। एक लाइन माथि प्रदर्शित एक गणक एक साधारण, छाडा, वा सरल अंश हुन्छन् र एक गैर-शून्य डिनोमिनेटर, लाइन तल देखाइएको। न्यूमरेटर र डिनोमिनेटर्स भिन्नहरुमा पनि प्रयोग गरिन्छ जुन सामान्य छैन, जसमा कम्पाउन्ड फ्र्याक्सन, जटिल अंशहरू, र मिश्रित अंकहरू समावेश छन्।
अंकगणित समारोह: संख्या सिद्धान्तमा, एक अंकगणित , अंकगणित , वा संख्या-सैद्धांतिक प्रकार्य अधिकांश लेखकहरूको लागि कुनै प्रकार्य f ( n ) हो जसको डोमेन धनात्मक पूर्णाgers्क हो र जसको दायरा जटिल संख्याहरूको सबसेट हो। हार्डी र राइटले उनीहरूको परिभाषामा आवश्यकतालाई समावेश गर्दछ कि एक अंकगणित समारोहले " n को केही अंकगणित गुण व्यक्त गर्दछ"।
अंकगणित समारोह: संख्या सिद्धान्तमा, एक अंकगणित , अंकगणित , वा संख्या-सैद्धांतिक प्रकार्य अधिकांश लेखकहरूको लागि कुनै प्रकार्य f ( n ) हो जसको डोमेन धनात्मक पूर्णाgers्क हो र जसको दायरा जटिल संख्याहरूको सबसेट हो। हार्डी र राइटले उनीहरूको परिभाषामा आवश्यकतालाई समावेश गर्दछ कि एक अंकगणित समारोहले " n को केही अंकगणित गुण व्यक्त गर्दछ"।
अंकगणित जीनस: गणितमा, बीजगणित प्रजातिको अंकगणित जीनस एक बीजगणित कर्भ वा Riemann सतह को जीनस को केहि सम्भावित सामान्यीकरण हो।
अंकगणित – ज्यामितीय मतलब: गणितमा, अंकगणित – ज्यामितीय माने दुई सकारात्मक वास्तविक संख्या x र y परिभाषित गरिएको छ:
अंकगणित ज्यामिति: गणितमा, अंकगणित ज्यामिति लगभग बीजगणित ज्यामिति देखि संख्या सिद्धान्त मा समस्या गर्न प्रविधिको उपयोग हो। अंकगणित ज्यामिति डायफान्टिन ज्यामितीयको वरिपरि केन्द्रित हुन्छ, बीजगणित प्रजातिहरूका तर्कसंगत बिन्दुहरूको अध्ययन।
अंकगणित समूह: गणितमा, अंकगणित समूह एउटा समूह हो जसलाई बीजगणित समूहको पूर्णांक अंकको रूपमा प्राप्त गरिन्छ, उदाहरणका लागि। तिनीहरू संख्याको सिद्धान्तमा क्वाड्रैटिक फार्महरू र अन्य शास्त्रीय विषयहरूको गणित गुणहरूको अध्ययनमा स्वाभाविक रूपमा उत्पन्न हुन्छन्। तिनीहरू पनि Riemannian manifolds को धेरै चाखलाग्दो उदाहरण को जन्म दिन्छ र त्यसैले भिन्न भिन्न ज्यामिति र टोपोलजी मा रुचि को वस्तुहरु हो। अन्तमा यी दुई विषयहरू अटोमोर्फिक फारमहरूको सिद्धान्तमा सामेल हुन्छन् जुन आधुनिक संख्याको सिद्धान्तमा मौलिक छ।
लिनियर प्रकार्य: गणितमा, प line्क्ति लाईन कार्यले दुई भिन्न तर सम्बन्धित धारणालाई बुझाउँदछ: क्यालकुलस र सम्बन्धित क्षेत्रहरूमा, एक रैखिक प्रकार्य एउटा फंक्शन हो जसको ग्राफ एक सीधा रेखा हो, जुन डिग्री शून्य वा एउटाको बहुपद फंक्शन हो। अन्य अवधारणाबाट त्यस्ता रैखिक प्रकार्य छुट्याउन, शब्द affine प्रकार्य अक्सर प्रयोग गरिन्छ। रेखीय बीजगणित, गणितीय विश्लेषण, र कार्यात्मक विश्लेषणमा, एक रैखिक प्रकार्य एक रेखाचित्र नक्शा हो।
ज्यामितीय मतलब: गणितमा, ज्यामितीय माध्य एक माध्य या औसत हो, जसले केन्द्रीय प्रवृत्ति वा संख्याको सेटको विशिष्ट मानलाई तिनीहरूको मानहरूको उत्पादन प्रयोग गरेर संकेत गर्दछ। Geometric माध्य संख्या 1 एक्स को एक सेट को लागि, N संख्या, अर्थात् को उत्पादन को N औं मूल रूपमा परिभाषित गरिएको छ, एक्स 2, ..., N, geometric माध्य रूपमा परिभाषित गरिएको छ x
अंकगणित पदानुक्रम: गणितीय तर्कमा, अंकगणित पदानुक्रम , अंकगणित पदानुक्रम वा क्लाइन - मोस्तोस्की पदानुक्रम निश्चित सेटहरूको वर्गीकरण गर्दछ सूत्रहरूको जटिलताको आधारमा जसले तिनीहरूलाई परिभाषित गर्दछ। कुनै वर्गीकरण प्राप्त गर्ने कुनै पनि सेटलाई अंकगणित भनिन्छ।
अंकगणित हाइपरबोलिक--मनिफोल्ड: गणितमा, स्पष्ट रूपमा समूह सिद्धान्त र हाइपरबोलिक ज्यामितिमा, अंकगणित क्लेनियन समूह क्लेटरियन समूहहरूको विशेष वर्ग हुन् जुन क्वाटरियन बीजगणितमा आदेश प्रयोग गरेर निर्माण गरिएको थियो। तिनीहरू अंकगणित समूहहरूका विशेष उदाहरणहरू हुन्। एक अंकगणित हाइपरबोलिक तीन-मनिफोल्ड हाइपरबोलिक स्पेसको भागफल हो एक अंकगणित क्लेनियन समूह द्वारा। यी मनिफोल्डहरूले केही विशेष रूपमा सुन्दर वा उल्लेखनीय उदाहरणहरू समावेश गर्दछ।
अंकगणित Fuchsian समूह: अंकगणित फुचियन समूह फुचियन समूहहरूको विशेष वर्ग हो जुन क्वाटरियन बीजगणितहरूमा अर्डरको प्रयोग गरेर निर्माण गरियो। तिनीहरू अंकगणित समूहहरूका विशेष उदाहरणहरू हुन्। अंकगणित Fuchsian समूह को प्रोटोटाइपिकल उदाहरण मोड्युलर समूह हो । तिनीहरू, र हाइपरबोलिक सतहले तिनीहरूको हाइपरबोलिक प्लेनमा तिनीहरूको कार्यसँग सम्बन्धित प्रायः फुसियन समूहहरू र हाइपरबोलिक सतहहरू बीच नियमित व्यवहार प्रदर्शन गर्दछ।
अंकगणित IF: अंकगणित IF कथन एक तीन तरणित अंकगणित कन्डिसन कथन हो, जुन १ 195 7 in मा फोर्ट्रानको पहिलो विमोचनमा पहिलो पटक देखीएको थियो, र पछि सबै संस्करणहरूमा फेला पर्‍यो, र केही अन्य प्रोग्रामिंग भाषाहरू, जस्तै FOCAL। तार्किक IF कथन अन्य भाषाहरूमा देखीएको विपरीत, फोर्ट्रान स्टेटमेन्टले तीन फरक शाखालाई परिभाषित गर्छ कि एक अभिव्यक्तिको नतीजा नकारात्मक, शून्य, वा सकारात्मक छ भने, क्रम अनुसार:
गणित कला मा नौ अध्याय: द गणित कलामा नौ अध्यायहरू चिनियाँ गणित पुस्तक हो, जुन १० औं दोस्रो शताब्दी ईसापूर्वका विद्वानहरूको धेरै पुस्ताले लेखेका थिए जुन यसको अन्तिम चरण दोस्रो शताब्दी सा.यु. यो पुस्तक चीनको प्रारम्भिक अस्तित्वमा रहेका गणित ग्रंथहरु मध्ये एक हो, पहिलो सुवान शु शु र झुबी सुजिंग । यसले गणितको दृष्टिकोण प्रस्तुत गर्दछ जुन समस्या समाधान गर्ने सबैभन्दा सामान्य विधिहरू पत्ता लगाउने केन्द्रमा रहेको छ जुन पुरानो ग्रीकको गणितज्ञहरुमा देखिएको सामान्य दृष्टिकोणसँग तुलना गर्न सकिदैन, जसले शुरुआती अक्षहरुबाट प्रस्तावहरु घटाउने प्रवृत्ति राख्थे।
सीमित क्षेत्र अंकगणित: गणितमा, परिमित क्षेत्र अंकगणित अंकगणित हो एक सीमित क्षेत्रमा विरूद्द गणित भन्दा विपरीत क्षेत्रको असीमित स with्ख्याको संख्याको तर्कसंगत संख्याको क्षेत्र जस्ता।
गणित कला मा नौ अध्याय: द गणित कलामा नौ अध्यायहरू चिनियाँ गणित पुस्तक हो, जुन १० औं दोस्रो शताब्दी ईसापूर्वका विद्वानहरूको धेरै पुस्ताले लेखेका थिए जुन यसको अन्तिम चरण दोस्रो शताब्दी सा.यु. यो पुस्तक चीनको प्रारम्भिक अस्तित्वमा रहेका गणित ग्रंथहरु मध्ये एक हो, पहिलो सुवान शु शु र झुबी सुजिंग । यसले गणितको दृष्टिकोण प्रस्तुत गर्दछ जुन समस्या समाधान गर्ने सबैभन्दा सामान्य विधिहरू पत्ता लगाउने केन्द्रमा रहेको छ जुन पुरानो ग्रीकको गणितज्ञहरुमा देखिएको सामान्य दृष्टिकोणसँग तुलना गर्न सकिदैन, जसले शुरुआती अक्षहरुबाट प्रस्तावहरु घटाउने प्रवृत्ति राख्थे।
रूफलाइन मोडेल: रूफलाइन मोडेल एक सहज ज्ञान प्रदर्शन मोडल हो जुन एक निश्चित कम्प्युट कर्नेलको प्रदर्शन अनुमान प्रदान गर्न प्रयोग गरिन्छ वा बहु-कोर, धेरै-कोर, वा एक्सेलेटर प्रोसेसर आर्किटेक्चरमा चलिरहेको, अन्तर्निहित हार्डवेयर सीमितताहरू, र सम्भावित लाभ र अनुकूलनको प्राथमिकता देखाउँदै। एकल प्रदर्शन आंकडामा स्थानीयता, ब्यान्डविथ, र बिभिन्न समानुतीकरणको ढाँचा संयोजन गरेर, नमूना प्राप्त प्रदर्शनको गुणस्तरको आकलन गर्न एक प्रभावशाली विकल्प हुनसक्दछ साधारण प्रतिशतको शिखर अनुमान प्रयोग गर्नुको सट्टा, यसले कार्यान्वयन र दुबै अन्तर्दृष्टि प्रदान गर्दछ। अन्तर्निहित प्रदर्शन सीमाहरू।
गुणन व्युत्क्रम: गणित, एक को multiplicative inverse वा एक नम्बर x को लागि पारस्परिक, 1 / एक्स वा एक्स -1, एक्स ले गुणन गर्दा जो एक नम्बर को multiplicative पहिचान, 1 एक अंश एक को multiplicative inverse / ख छ ख पैदावार छ / द्वारा denoted a वास्तविक संख्याको गुणाकार व्युत्क्रमको लागि, संख्याबाट १ विभाजन गर्नुहोस्। उदाहरण को लागी, rec को reciprocal एक पाँचौं हो, र ०.२5 को reciprocal १ लाई ०.२5, वा 4. द्वारा विभाजित गर्दछ। reciprocal फंक्शन , प्रकार्य f ( x ) जुन x लाई १ / x मा नक्शा दिन्छ, यसको एक साधारण उदाहरण हो। प्रकार्य जुन यसको आफ्नै व्युत्क्रम हो।
जाली (अलग उपसमूह): लाई थ्योरी र गणित सम्बन्धी क्षेत्रहरुमा, स्थानीय कम्पेक्ट समूहमा एक जाली सम्पत्तीको साथ एक छुट्टै उपसमूह हो जुन भागफलको स्पेसमा परिमित इन्वाइरेन्ट मापन हुन्छ। आर एन को उपसमूहको विशेष अवस्थामा, यो पोट्टिको आवधिक उपसेटको रूपमा जालीको सामान्य ज्यामितीय धारणा बराबर हो, र ल्याटिक्सको बीजगणित संरचना र सबै ल्याटिक्सको स्पेसको ज्यामिति दुबै तुलनात्मक रूपमा राम्रोसँग बुझ्न सकिन्छ।
डिसकल्कुलिया: डिसकलकुलिया एक अपा .्गता हो जसको परिणाम स्वरूप अंकगणित सिक्न वा बुझ्न, जस्तै संख्या बुझ्ने कठिनाई, संख्या कसरी चलाउने सिक्ने, गणित गणना गर्ने र गणितमा तथ्यहरू सिक्ने। यसलाई कहिलेकाँही अनौपचारिक रूपमा "गणित डिस्लेक्सिया" भनेर पनि चिनिन्छ, यद्यपि यो भ्रमपूर्ण हुन सक्छ किनकि डिस्लेक्सिया डिस्क्लकुलिया भन्दा फरक अवस्था हो।
अंकगणित शिफ्ट: कम्प्युटर प्रोग्रामिंगमा, अंकगणित शिफ्ट शिफ्ट अपरेटर हो, कहिलेकाँही हस्ताक्षर गरिएको पाली पनि भनिन्छ । दुई आधारभूत प्रकारहरू अंकगणित बायाँ सिफ्ट र अंकगणित दायाँ पाली हो । बाइनरी नम्बरहरूका लागि यो बिटवाईज अपरेसन हो जसले यसको अपरेन्डको सबै बिट्सहरू बदल्छ; अपरेन्डमा प्रत्येक बिट केवल दिइएको बिट पोष्टहरूको स moved्ख्यामा सारिन्छ, र खाली बिट-पोजिशन्स् भरिन्छ। सबै ० सेकेन्ड भर्नको सट्टा तार्किक शिफ्टमा, दायाँ सर्दा, बायाँतिरको बिटमा प्रतिलिपि हुन्छ सबै खाली पदहरू भर्नुहोस्।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाई (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (CPU), FPUs, र ग्राफिक्स प्रसंस्करण एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
पास्कल क्यालकुलेटर: पास्कल क्यालकुलेटर एक मेकानिकल क्यालकुलेटर हो जुन ब्लेज पास्कलले १ 17 औं शताब्दीको बीचमा आविष्कार गरेको थियो। पास्कललाई बुबाको काम रूईनमा करको पर्यवेक्षकको रूपमा आवश्यक पर्ने परिगणित गणित गणना द्वारा एक क्यालकुलेटर विकास गर्न नेतृत्व गरिएको थियो। उनले मेसिन डिजाइन गरी दुई संख्याहरू सिधै थप्न र घटाउन र दोहोर्याइएको जोड वा घटाउ मार्फत गुणा र भाग प्रदर्शन गर्न।
अंकगणित माध्य: गणित र तथ्या .्कमा , अंकगणित माध्य , वा साधारण माध्य वा औसत , स numbers्ग्रहमा संख्याहरूको गणना द्वारा विभाजित संख्याको संग्रहको योग हो। संग्रह प्राय: प्रयोगको परीक्षण वा अवलोकनात्मक अध्ययनको नतीजाको सेट हो, वा प्रायः सर्वेक्षणहरूबाट परिणामहरूको सेट हुन्छ। गणित र तथ्या .्कको केही प्रस in्गमा "अंकगणित मीन" भन्ने शव्दलाई प्राथमिकता दिइन्छ, किनकि यसले ज्यामितीय माध्य र हार्मोनिक मध्य जस्ता अन्य माध्यमहरू भन्दा यसलाई छुट्याउन मद्दत गर्दछ।
अंकगणित र ज्यामितीय साधनको असमानता: गणितमा, अंकगणित र ज्यामितीय साधनको असमानता , वा अधिक संक्षेपमा एएम – जीएम असमानता , बताउँछ कि गैर-नकारात्मक वास्तविक संख्याहरूको सूचीको अंकगणित माध्य एउटै सूचीको ज्यामितीय मतलब भन्दा ठूलो वा बराबर हो; र अगाडि, ती दुई साधनहरू बराबर छन् र मात्र यदि सूचीमा प्रत्येक संख्या समान छ।
सामान्य (गणित): गणितमा, एक आदर्श एक वास्तविक वा जटिल भेक्टर स्पेसबाट nonnegative वास्तविक संख्या सम्मिलित कार्य हो जुन उत्पत्तिबाट दूरी जस्तै केही तरिकामा व्यवहार गर्दछ: यो स्केलिंगको साथ कम्युट हुन्छ, त्रिकोण असमानताको एक रूप मान्दछ, र शून्य मात्र हुन्छ उत्पत्ति विशेष रूपमा भेक्टरको युक्लिडियन दूरी उत्पत्तिदेखि नै एउटा आदर्श हो, यसलाई युक्लिडियन नॉर्म वा २-नॉर्म भनिन्छ, जुन आफैसँगै भेक्टरको भित्री उत्पादनको वर्गमूल पनि हो।
अंकगणित संख्या: संख्या सिद्धान्त मा, एक अंकगणित संख्या एक पूर्णांक हो जसको लागि यसको सकारात्मक भाजक को औसत एक पूर्णांक हो। उदाहरण को लागी, 6 अंकगणित संख्या हो किनकि यसको भाजक को औसत छ
एक हत्याको अंकगणित: एक हत्याको अंकगणती १ 199 199 १ दिमित्री स्वेतोजारो द्वारा निर्देशित सोभियत क्रिम फिल्म हो।
एबेलियन प्रजातिहरूको अंकगणित: गणितमा, एबेलियन प्रजातिहरूको अंकगणित भनेको एबेलियन प्रजातिको संख्या सिद्धान्त वा एबेलियन प्रजातिहरूको परिवारको अध्ययन हो। यो पियरे डि फर्मेटको अध्ययनमा फर्कन्छ जुन अब अण्डाकार वक्रका रूपमा चिनिन्छ; परिणाम र अनुमान दुवैको हिसाबले गणित ज्यामिति को एक धेरै पर्याप्त क्षेत्र भएको छ। यी मध्ये धेरै जसो एउटा एबेलियन प्रजाति A को लागी एक संख्या क्षेत्र K माथि प्रस्तुत गर्न सकिन्छ; वा अधिक सामान्यतया।
एबेलियन प्रजातिहरूको अंकगणित: गणितमा, एबेलियन प्रजातिहरूको अंकगणित भनेको एबेलियन प्रजातिको संख्या सिद्धान्त वा एबेलियन प्रजातिहरूको परिवारको अध्ययन हो। यो पियरे डि फर्मेटको अध्ययनमा फर्कन्छ जुन अब अण्डाकार वक्रका रूपमा चिनिन्छ; परिणाम र अनुमान दुवैको हिसाबले गणित ज्यामिति को एक धेरै पर्याप्त क्षेत्र भएको छ। यी मध्ये धेरै जसो एउटा एबेलियन प्रजाति A को लागी एक संख्या क्षेत्र K माथि प्रस्तुत गर्न सकिन्छ; वा अधिक सामान्यतया।
एबेलियन प्रजातिहरूको अंकगणित: गणितमा, एबेलियन प्रजातिहरूको अंकगणित भनेको एबेलियन प्रजातिको संख्या सिद्धान्त वा एबेलियन प्रजातिहरूको परिवारको अध्ययन हो। यो पियरे डि फर्मेटको अध्ययनमा फर्कन्छ जुन अब अण्डाकार वक्रका रूपमा चिनिन्छ; परिणाम र अनुमान दुवैको हिसाबले गणित ज्यामिति को एक धेरै पर्याप्त क्षेत्र भएको छ। यी मध्ये धेरै जसो एउटा एबेलियन प्रजाति A को लागी एक संख्या क्षेत्र K माथि प्रस्तुत गर्न सकिन्छ; वा अधिक सामान्यतया।
सीमित क्षेत्र अंकगणित: गणितमा, परिमित क्षेत्र अंकगणित अंकगणित हो एक सीमित क्षेत्रमा विरूद्द गणित भन्दा विपरीत क्षेत्रको असीमित स with्ख्याको संख्याको तर्कसंगत संख्याको क्षेत्र जस्ता।
साधारण अंकगणित: सेट सिद्धान्तको गणितीय क्षेत्रमा, अण्डिनल अंकगणितले सामान्य संख्यामा तीन सामान्य अपरेसनहरू वर्णन गर्दछ: थप, गुणन, र घटाई। प्रत्येकलाई दुईवटा फरक तरिकाले परिभाषित गर्न सकिन्छ: या त स्पष्ट रूपमा व्यवस्थित सेट निर्माण गरेर जुन अपरेशनको परिणाम प्रतिनिधित्व गर्दछ वा ट्रान्सफाइमन्ट रिकर्सन प्रयोग गरेर। क्यान्टर सामान्य फारामले अध्यादेश लेखनको एक मानक तरीका प्रदान गर्दछ। यी सामान्य ऑर्डिनल अपरेशन्सको अतिरिक्त, त्यहाँ "प्राकृतिक" अंकगणित र निम्बर अपरेशनहरू छन्।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - जोड, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निकासी। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई गणितको गणितको एक उच्च स्तरको विभाजन मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरुसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
पूर्णांक ओभरफ्लो: कम्प्युटर प्रोग्रामिंगमा, पूर्णांक ओभरफ्लो हुन्छ जब अंकगणित आपरेशनले संख्यात्मक मान सिर्जना गर्न कोसिस गर्दछ जुन दायराभन्दा बाहिरको हुन्छ जसलाई दिइएको अंकको संख्यासँग प्रतिनिधित्व गर्न सकिन्छ - या त अधिकतम वा न्यूनतम प्रतिनिधित्व मान भन्दा कम।
P-adic L- प्रकार्य: गणितमा, p -adic zeta प्रकार्य , वा अधिक सामान्यतया p -adic L -function , समारोह Riemann zeta प्रकार्य, वा अधिक सामान्य L -function को समान , तर जसको डोमेन र लक्ष्य p-adic हो । उदाहरणका लागि, डोमेन पृ -adic पूर्णाङ्कहरुको Z पी, एक profinite पृ -group, वा Galois प्रतिनिधित्व को एक पी -adic परिवार हुन सक्छ, र छवि पृ -adic संख्या क्यू पी वा यसको बीजीय बन्द हुन सक्छ।
महत्त्वपूर्ण आंकडा: स्थितिगत संकेतन मा एक संख्या को महत्वपूर्ण आंकड़े संख्या मा विश्वसनीय छन् र केहि को मात्रा संकेत गर्न एकदम आवश्यक छ कि अंक मा अंक हो। यदि कुनै मापनको नतीजा अभिव्यक्त गर्ने संख्यासँग मापन रिजोलुसनले अनुमति दिएको अ than्कहरू भन्दा बढी अंकहरू छन् भने, मापन रिजोलुसनले अनुमति दिएको अ reliable्क ​​मात्र भरपर्दो छ त्यसैले मात्र यी महत्त्वपूर्ण तथ्या .्कहरू हुन सक्छन्। उदाहरण को लागी, यदि एक लम्बाई मापन ११4..8 मिमी दिन्छ जबकि मापन मा प्रयोग गरीन्छ शासक मा अंक को बीचको सबैभन्दा सानो अन्तराल १ मिमी छ, तब पहिलो तीन अंक मात्र भरपर्दो छ त्यसैले महत्त्वपूर्ण आंकडा हुन सक्छ। यी अंकहरू मध्ये, अन्तिम अंकमा अनिश्चितता छ तर यसलाई महत्त्वपूर्ण फिगरको रूपमा पनि लिइन्छ किनकि अनिश्चित तर भरपर्दो अंकहरूलाई महत्त्वपूर्ण अंक मानिन्छ। अर्को उदाहरण २.9 L एलको भोल्युम मापन हो जुन ± ०.० L एलको अनिश्चितताको साथ छ। वास्तविक खण्ड कतै २.9 L एल र 3.0.०3 एलको बीचमा छ। यदि सबै तीन अ certain्कहरू निश्चित नभए पनि भरपर्दो छ किनकि यी स्वीकार्य अनिश्चितताको साथ वास्तविक खण्डमा संकेत गर्दछ। । त्यसो भए यी महत्त्वका आंकडा हुन्।