Arithmetic progression, Ring (mathematics), Arithmetical hierarchy

अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको गणित प्रगति हो जसमा २ को फरक फरक हुन्छ।
रिंग (गणित): गणितमा, रिंगहरू बीजगणित संरचनाहरू हुन् जसले फिल्ड्सलाई सामान्यीकृत गर्दछ: गुणन कम्युटेटिभ हुनु हुँदैन र गुणात्मक ईन्वर्सहरू अवस्थित हुनुपर्दैन। अर्को शब्दमा, एउटा औंठी दुई सेट बाइनरी अपरेशनहरू सन्तुष्ट पार्ने गुणहरूसँग मिल्दो सेट हो जुन पूर्णांकहरूको थप र गुणनको लागि समान हुन्छ। अंगूठी तत्वहरू संख्या हुन सक्छ जस्तै पूर्णांक वा जटिल संख्या, तर तिनीहरू गैर-संख्यात्मक वस्तुहरू पनि हुन सक्छन् जस्तै बहुपदहरू, वर्ग मैट्रिकहरू, प्रकार्यहरू, र शक्ति श्रृंखला।
अंकगणित पदानुक्रम: गणितीय तर्कमा, अंकगणित पदानुक्रम , अंकगणित पदानुक्रम वा क्लाइन - मोस्तोस्की पदानुक्रम निश्चित सूत्रहरूको परिभाषित गर्ने सूत्रहरूको जटिलताको आधारमा वर्गीकृत गर्दछ। कुनै वर्गीकरण प्राप्त गर्ने कुनै पनि सेटलाई अंकगणित भनिन्छ।
फिर्ताको दर: वित्त मा, फिर्ती एक लगानी मा एक लाभ हो। यसले लगानीको मूल्यमा कुनै परिवर्तन, र / वा नगदी प्रवाह समावेश गर्दछ जुन लगानीकर्ताले ब्याज भुक्तान, कुपन, नगद लाभांश, स्टक लाभांश वा व्युत्पन्न वा संरचित उत्पादबाट भुक्तान जस्ता लगानीबाट प्राप्त गर्दछ। यो कि त पूर्ण सर्तमा वा लगानीको रकमको प्रतिशतको रूपमा मापन गर्न सकिन्छ। पछिल्लोलाई होल्डिंग पिरियड रिटर्न पनि भनिन्छ।
अंकगणित शिफ्ट: कम्प्युटर प्रोग्रामिंगमा, अंकगणित शिफ्ट शिफ्ट अपरेटर हो, कहिलेकाँही हस्ताक्षर शिफ्ट पनि भनिन्छ । दुई आधारभूत प्रकारहरू अंकगणित बायाँ सिफ्ट र अंकगणित दायाँ सिफ्ट हुन् । बाइनरी नम्बरहरूका लागि यो बिटवाईज अपरेसन हो जसले यसको अपरेन्डको सबै बिट्स सार्दछ; अपरेन्डमा प्रत्येक बिट केवल दिइएको बिट पोष्टहरूको स moved्ख्यामा सारिन्छ, र खाली बिट-पोजिशन्स भरिन्छ। सबै ० सेकेन्ड भर्नको सट्टा तार्किक शिफ्टमा, दायाँ सर्दा, बायाँतिरको बिटमा प्रतिलिपि हुन्छ सबै खाली पदहरू भर्नुहोस्।
अंकगणित रि ring बीजगणितमा, एउटा कम्युटिभ रिंग आर अंकगणित हो भनिन्छ यदि निम्न कुनै पनि बराबर सर्तहरू राख्छ भने: स्थानीयकरण को आर प्रत्येक अधिकतम आदर्शको लागि एक अis्गालीय ringण हो R को सबै आदर्शका लागि , र , सबै आदर्शका लागि , र ,
अंकगणित डोरी: अंकगणित रस्सी , वा गाँठिएको डोरी मध्य युगमा व्यापक रूपमा प्रयोग गरिएको गणित उपकरण थियो जुन धेरै गणितीय र ज्यामितीय समस्या समाधान गर्न प्रयोग गर्न सकिन्छ।
अराकेलोभ सिद्धान्त: गणितमा, अरकेलोभ सिद्धान्त डायओफान्टिन ज्यामितिमा एक दृष्टिकोण हो, सुरेन अरकेलोभको लागि नामकरण गरिएको। यो उच्च आयाममा डियोफ्यान्टाइन समीकरणहरूको अध्ययन गर्न प्रयोग गरिन्छ।
सार विश्लेषणात्मक संख्या सिद्धान्त: एब्स्ट्र्याक्ट एनालिटिक्स नम्बर थ्योरी भनेको गणितको एक शाखा हो जसले शास्त्रीय विश्लेषणात्मक संख्या सिद्धान्तको विचारहरू र प्रविधिहरू लिन्छ र तिनीहरूलाई विभिन्न गणितीय क्षेत्रहरूमा विभिन्न प्रकारका लागि लागू गर्दछ। शास्त्रीय प्राइम नम्बर प्रमेय प्रोटोटाइपिकल उदाहरणको रूपमा कार्य गर्दछ, र अमूर्त एसिम्पोटिक वितरण परिणामहरूमा जोड दिइन्छ। यो सिद्धान्त बीसौं शताब्दीमा जोन नोपफमेकर र अर्न बेउरलिंग जस्ता गणितज्ञहरूले आविष्कार र विकास गरेका थिए।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको गणित प्रगति हो जसमा २ को फरक फरक हुन्छ।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको गणित प्रगति हो जसमा २ को फरक फरक हुन्छ।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
अंकगणित शिफ्ट: कम्प्युटर प्रोग्रामिंगमा, अंकगणित शिफ्ट शिफ्ट अपरेटर हो, कहिलेकाँही हस्ताक्षर शिफ्ट पनि भनिन्छ । दुई आधारभूत प्रकारहरू अंकगणित बायाँ सिफ्ट र अंकगणित दायाँ सिफ्ट हुन् । बाइनरी नम्बरहरूका लागि यो बिटवाईज अपरेसन हो जसले यसको अपरेन्डको सबै बिट्स सार्दछ; अपरेन्डमा प्रत्येक बिट केवल दिइएको बिट पोष्टहरूको स moved्ख्यामा सारिन्छ, र खाली बिट-पोजिशन्स भरिन्छ। सबै ० सेकेन्ड भर्नको सट्टा तार्किक शिफ्टमा, दायाँ सर्दा, बायाँतिरको बिटमा प्रतिलिपि हुन्छ सबै खाली पदहरू भर्नुहोस्।
मानसिक गणना: मानसिक गणनामा कुनै पनि आपूर्ति वा उपकरणहरू जस्तै कुनै क्यालकुलेटरको कुनै सहयोग बिना, मानव मस्तिष्कको प्रयोग गरेर अंकगणित गणना हुन्छ। जब कम्प्युटि tools उपकरणहरू उपलब्ध हुँदैनन्, मानिसहरू मानसिक गणना प्रयोग गर्छन्, जब यो गणनाको अन्य माध्यमहरू भन्दा छिटो हुन्छ, वा प्रतिस्पर्धी प्रस in्गमा पनि। मानसिक गणनामा अक्सर विशेष प्रकारको समस्याहरूको लागि बनाइएको विशिष्ट प्रविधिहरूको प्रयोग समावेश गर्दछ। मानसिक गणना गर्न असामान्य रूपमा उच्च क्षमता भएका मानिसहरूलाई मानसिक क्यालकुलेटर वा बिजुली क्यालकुलेटर s भनिन्छ।
मानसिक गणना: मानसिक गणनामा कुनै पनि आपूर्ति वा उपकरणहरू जस्तै कुनै क्यालकुलेटरको कुनै सहयोग बिना, मानव मस्तिष्कको प्रयोग गरेर अंकगणित गणना हुन्छ। जब कम्प्युटि tools उपकरणहरू उपलब्ध हुँदैनन्, मानिसहरू मानसिक गणना प्रयोग गर्छन्, जब यो गणनाको अन्य माध्यमहरू भन्दा छिटो हुन्छ, वा प्रतिस्पर्धी प्रस in्गमा पनि। मानसिक गणनामा अक्सर विशेष प्रकारको समस्याहरूको लागि बनाइएको विशिष्ट प्रविधिहरूको प्रयोग समावेश गर्दछ। मानसिक गणना गर्न असामान्य रूपमा उच्च क्षमता भएका मानिसहरूलाई मानसिक क्यालकुलेटर वा बिजुली क्यालकुलेटर s भनिन्छ।
आवाज: तर्कमा, अधिक स्पष्ट रूपमा डिडक्टिव तर्कमा, एक तर्क ध्वनि हुन्छ यदि यो दुबै फारममा मान्य छ र यसको परिसर सत्य छ। ध्वनीको गणित तर्कमा पनि सम्बन्धित अर्थ छ, जहाँ तार्किक प्रणालीहरु ध्वनी छन् यदि केवल प्रणालीमा प्रमाणित गर्न सकिने प्रत्येक सूत्र प्रणालीको शब्दार्थको सम्बन्धमा तार्किक रुपमा मान्य छ।
आर्किमेडियन सर्पिल: अर्चिमिडियन सर्पिल एक सर्पिल हो जुन तेस्रो शताब्दी ईसा पूर्व ग्रीक गणितज्ञ आर्किमिडीजको नाम हो। यो स्थिर स्थानबाट स्थिर रेखाको साथ एक रेखाको साथ टाढा सर्ने विन्दुको समयको साथ स्थानहरूमा अनुरूप लोकोस हो जुन स्थिर कुनात्मक वेगको साथ घुम्दछ। बराबर, ध्रुव निर्देशांक ( r , θ ) मा यो समीकरण द्वारा वर्णन गर्न सकिन्छ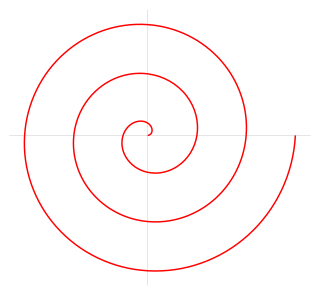
अंकगणित समूह: गणितमा, अंकगणित समूह एउटा समूह हो जसलाई बीजगणितीय समूहको पूर्णांक अंकको रूपमा प्राप्त गरिन्छ, उदाहरणका लागि। तिनीहरू संख्या सिद्धान्त मा क्वाडरेटिक फार्म र अन्य शास्त्रीय विषयहरु को अंकगणित गुणहरु को अध्ययन मा स्वाभाविक रूपमा उठ्छ। तिनीहरू पनि Riemannian manifolds को धेरै चाखलाग्दो उदाहरण को जन्म दिन्छन् र त्यसैले भिन्न भिन्न ज्यामिति र टोपोलजी मा रूचि को वस्तुहरु छन्। अन्तमा यी दुई विषयहरू अटोमोर्फिक फारमहरूको सिद्धान्तमा सामेल हुन्छन् जुन आधुनिक संख्याको सिद्धान्तमा मौलिक छ।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको गणित प्रगति हो जसमा २ को फरक फरक हुन्छ।
अंकगणित सतह: गणितमा, फ्रडेक्स क्षेत्रको साथ डेडेकिन्ड डोमेन आर माथि अंकगणित सतह एक ज्यामितीय वस्तु एक पारंपरिक आयाम, र एक अन्य आयाम प्राइमन्स को असीमित द्वारा प्रदान गरीएको हो। जब आर पूर्णांक Z को औंठी हो, यो अन्तर्ज्ञान मुख्य रेखा स्पेक्ट्रम स्पेस ( Z ) लाई रेखाको समान देखीरहेको हुन्छ। अंकगणित सतहहरू डायफान्टिन ज्यामितिमा स्वाभाविक रूपमा देखा पर्दछ, जब K लाई परिभाषित एक बीजगणित कर्भ क्षेत्र R / P मा घटाइएको छ भन्ने सोच्दछ, जहाँ P सबै भन्दा P को R को एक आदर्श आदर्श हो; र R / P लाई घटाउने प्रक्रियाको बारेमा के हुन्छ भनेर निर्दिष्ट गर्न सहयोग पुर्‍याउँछ जब सबै भन्दा भोला बाटोले अर्थ प्राप्त गर्न असफल हुन्छ।
अंकगणित टोपोलजी: अंकगणित टोपोलजी गणितको क्षेत्र हो जुन बीजगणित संख्या सिद्धान्त र टोपोलजीको संयोजन हो। यो संख्या क्षेत्रहरू र बन्द, orientable--manifolds बीच समानता स्थापना गर्दछ।
Coxeter - Dynkin आरेख: ज्यामितिमा, Coxeter - Dynkin रेखाचित्र संख्यात्मक लेबल किनाराहरू सहितको ग्राफ हो जुन ऐनाको संग्रहको बीच स्थानिक सम्बन्ध प्रतिनिधित्व गर्दछ। यसले क्यालिडोस्कोपिक निर्माणको वर्णन गर्दछ: प्रत्येक ग्राफ "नोड" ले एक दर्पण प्रतिनिधित्व गर्दछ र एउटा शाखासँग जोडिएको लेबलले दुई दर्पणको बीचमा डिहेड्रल ए angle्गल अर्डर स enc्केतन गर्दछ, अर्थात्, परिमाण प्रतिबिम्ब बीचको कोणबाट १ 180० प्राप्त गर्न गुणा गर्न सकिने रकम डिग्री लेबल नगरिएको शाखाले स्पष्ट रूपमा आदेश-3 प्रतिनिधित्व गर्दछ।
अंकगणित भूमिगत: अंकगणित अन्डरफ्लो भनेको कम्प्युटर प्रोग्राममा एक अवस्था हो जहाँ गणनाको नतिजा कम्प्युटरको तुलनामा सानो सटीक मानको संख्या हो जुन वास्तविक रूपमा यसको केन्द्रीय प्रसंस्करण इकाई (सीपीयू) मा मेमोरीमा प्रतिनिधित्व गर्न सक्दछ।
अंकगणित विविधता: गणितमा, अंकगणित प्रजाति भनेको सम्बन्धित बीजगणित लाइ समूहको अंकगणित सब ग्रुप द्वारा हर्मिटियन सममेट्रिक स्पेसको भागफल अन्तर हो।
अंकगणित विविधता: गणितमा, अंकगणित प्रजाति भनेको सम्बन्धित बीजगणित लाइ समूहको अंकगणित सब ग्रुप द्वारा हर्मिटियन सममेट्रिक स्पेसको भागफल अन्तर हो।
अंकगणित zeta प्रकार्य: गणितमा, अंकगणित zeta प्रकार्य एक zeta समारोह हो जुन सीमावर्ती भन्दा राम्रो प्रकारको योजनासँग सम्बन्धित छ। अंकगणित zeta प्रकार्य Riemann zeta समारोह र Dedekind zeta प्रकार्य मा अधिक आयाम। अंकगणित zeta समारोह संख्या सिद्धान्त को एक सबै भन्दा मौलिक वस्तु हो।
अंकगणित: एरिथमेटिका गणितज्ञ मा एक प्राचीन ग्रीक पाठ हो जुन तेस्रो शताब्दी AD मा गणितज्ञ डायफन्टस द्वारा लेखिएको थियो। यो १ 130० बीजगणित समस्याहरूको संकलन हो कि निर्धारण समीकरण र अनिश्चित समीकरणहरूको संख्यात्मक समाधान दिन्छ।
जोन वालिस: जोन वालिस एक अंग्रेज पादरी र गणितज्ञ थिए जसलाई इन्फिनिसिमल क्यालकुलसको विकासको लागि आंशिक श्रेय दिइन्छ। १ 164343 र १89 89 ween बीचमा उनले संसद र पछि शाही अदालतका लागि प्रमुख क्रिप्टोग्राफरको रूपमा काम गरे। उनी प्रतीकको परिचय दिएका छन् - अनन्तको अवधारणा प्रतिनिधित्व गर्न। उस्तै प्रकार उसले १ / used एक infinitesim को लागी प्रयोग गर्‍यो। जोन वालिस, न्यूटनका समकालीन र गणितको प्रारम्भिक पुनर्जागरणका एक महान बौद्धिक व्यक्ति थिए।
हेनरी ब्रिग्स (गणितज्ञ): हेनरी ब्रिग्स एक अंग्रेजी गणितज्ञ थिए जोन नेपियरले आविष्कार गरेको मूल लगारिदमलाई सामान्य लोगारिथ्समा बदल्नका लागि उल्लेखनीय थियो, जुन कहिलेकाँहि उनको सम्मानमा ब्रिग्सियन लोगारिथ्स भनेर चिनिन्छ। आधुनिक प्रयोगमा लामो डिभिजनका लागि विशिष्ट एल्गोरिथ्म ब्रिग्स सी द्वारा प्रस्तुत गरिएको थियो । १00०० ई।
Arithmetica Universalis: एरिथमेटिका युनिभर्सलिस इसाक न्यूटन द्वारा गणित पाठ हो। ल्याटिन भाषामा लेखिएको यो क्याम्ब्रिज विश्वविद्यालयमा गणितको लुकासियन प्रोफेसरको रूपमा न्युटनको उत्तराधिकारी विलियम व्हिसनद्वारा सम्पादन र प्रकाशित गरिएको थियो। अरिथेटिका न्यूटनको लेक्चर नोटमा आधारित थियो।
दस कम्पनेशनल क्यानन: टेन कम्प्युटेसनल क्यानन भनेको दस चिनियाँ गणित कार्यहरूको स early्ग्रह हो जुन प्रारम्भिक टाasty राजवंश गणितज्ञ ली चुन्फेen (–०२-–70०) द्वारा गणितमा शाही परीक्षाका लागि आधिकारिक गणितको पाठको संकलन थियो।
दोस्रो अर्डर अंकगणित: गणितीय तर्कमा, दोस्रो अर्डर अंकगणित भनेको अक्सियोमेटिक प्रणालीको संग्रह हो जुन प्राकृतिक संख्याहरू र उनीहरूको सबसेटलाई औपचारिक बनाउँछ। यो धेरैको लागि एक आधार को रूप मा axiomatic सेट सिद्धान्त एक वैकल्पिक हो, तर सबै छैन, गणित को।
जर्ज मयूर: जर्ज पियर एफआरएस एक अंग्रेजी गणितज्ञ र ए Ang्गलिकन धर्मगुरु थिए। उनले ब्रिटिश बीजगणित भनिने तर्कको स्थापना गरे।
अंकगणित ज्यामिति: गणितमा, अंकगणित ज्यामिति लगभग बीजगणित ज्यामिति देखि संख्या सिद्धान्त मा समस्या गर्न प्रविधिको उपयोग हो। अंकगणित ज्यामिति डायओफान्टिन ज्यामितीयको वरिपरि केन्द्रित हुन्छ, बीजगणित प्रजातिहरूका तर्कसंगत बिन्दुहरूको अध्ययन।
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाइ (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (सीपीयू), FPUs, र ग्राफिक्स प्रोसेसिंग एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
दोस्रो अर्डर अंकगणित: गणितीय तर्कमा, दोस्रो अर्डर अंकगणित भनेको अक्सियोमेटिक प्रणालीको संग्रह हो जुन प्राकृतिक संख्याहरू र उनीहरूको सबसेटलाई औपचारिक बनाउँछ। यो धेरैको लागि एक आधार को रूप मा axiomatic सेट सिद्धान्त एक वैकल्पिक हो, तर सबै छैन, गणित को।
दोस्रो अर्डर अंकगणित: गणितीय तर्कमा, दोस्रो अर्डर अंकगणित भनेको अक्सियोमेटिक प्रणालीको संग्रह हो जुन प्राकृतिक संख्याहरू र उनीहरूको सबसेटलाई औपचारिक बनाउँछ। यो धेरैको लागि एक आधार को रूप मा axiomatic सेट सिद्धान्त एक वैकल्पिक हो, तर सबै छैन, गणित को।
सार विश्लेषणात्मक संख्या सिद्धान्त: एब्स्ट्र्याक्ट एनालिटिक्स नम्बर थ्योरी भनेको गणितको एक शाखा हो जसले शास्त्रीय विश्लेषणात्मक संख्या सिद्धान्तको विचारहरू र प्रविधिहरू लिन्छ र तिनीहरूलाई विभिन्न गणितीय क्षेत्रहरूमा विभिन्न प्रकारका लागि लागू गर्दछ। शास्त्रीय प्राइम नम्बर प्रमेय प्रोटोटाइपिकल उदाहरणको रूपमा कार्य गर्दछ, र अमूर्त एसिम्पोटिक वितरण परिणामहरूमा जोड दिइन्छ। यो सिद्धान्त बीसौं शताब्दीमा जोन नोपफमेकर र अर्न बेउरलिंग जस्ता गणितज्ञहरूले आविष्कार र विकास गरेका थिए।
अंकगणित समारोह: संख्या सिद्धान्तमा, एक अंकगणित , अंकगणित , वा संख्या-सैद्धांतिक प्रकार्य अधिकांश लेखकहरूको लागि कुनै प्रकार्य f ( n ) हो जसको डोमेन धनात्मक पूर्णाgers्क हो र जसको दायरा जटिल संख्याहरूको सबसेट हो। हार्डी र राइटले उनीहरूको परिभाषामा आवश्यकतालाई समावेश गर्दछ कि एक अंकगणित समारोहले " n को केही अंकगणित गुण व्यक्त गर्दछ"।
अंकगणित समारोह: संख्या सिद्धान्तमा, एक अंकगणित , अंकगणित , वा संख्या-सैद्धांतिक प्रकार्य अधिकांश लेखकहरूको लागि कुनै प्रकार्य f ( n ) हो जसको डोमेन धनात्मक पूर्णाgers्क हो र जसको दायरा जटिल संख्याहरूको सबसेट हो। हार्डी र राइटले उनीहरूको परिभाषामा आवश्यकतालाई समावेश गर्दछ कि एक अंकगणित समारोहले " n को केही अंकगणित गुण व्यक्त गर्दछ"।
अंकगणित पदानुक्रम: गणितीय तर्कमा, अंकगणित पदानुक्रम , अंकगणित पदानुक्रम वा क्लाइन - मोस्तोस्की पदानुक्रम निश्चित सूत्रहरूको परिभाषित गर्ने सूत्रहरूको जटिलताको आधारमा वर्गीकृत गर्दछ। कुनै वर्गीकरण प्राप्त गर्ने कुनै पनि सेटलाई अंकगणित भनिन्छ।
अंकगणित माध्य: गणित र तथ्या .्कमा , अंकगणित माध्य , वा साधारण माध्य वा औसत , स numbers्ग्रहमा संख्याहरूको गणना द्वारा विभाजित संख्याको संग्रहको योग हो। संग्रह प्राय: प्रयोगको परीक्षण वा अवलोकनात्मक अध्ययनको नतीजाको सेट हो, वा प्रायः सर्वेक्षणहरूबाट परिणामहरूको सेट हुन्छ। "अंकगणित मीन" भन्ने शव्दलाई गणित र तथ्या mean्कका केही प्रस preferred्गहरूमा प्राथमिकता दिइन्छ, किनकि यसले ज्यामितीय माध्य र हार्मोनिक मध्य जस्ता अन्य माध्यमहरू भन्दा फरक पार्न मद्दत गर्दछ।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - थप, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निष्कर्षण। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई आधुनिक गणितको शीर्ष-स्तर विभाजनहरू मध्ये एक मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरूसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित प्रगति: एक अंकगणित प्रगति (एपी) वा अंकगणित अनुक्रम संख्याहरूको अनुक्रम हो कि लगातार सर्तहरू बीचको फरक स्थिर हुन्छ। उदाहरण को लागी, अनुक्रम 5,,,,, ११, १,, १ ,. ,. २ अंकको गणित प्रगति हो जसमा २ को फरक फरक हुन्छ।
ओटोनलिटी र Utonality: Otonality र utonality क्रमशः, कर्डहरु जसको पिच कक्षाहरू दिइएको निश्चित टोन (पहिचान) को harmonics को वा subharmonics छन् वर्णन गर्न हैरी Partch द्वारा शुरू सर्तहरू छन्। उदाहरणका लागि: 1/1, 2/1, 3/1, ... वा 1/1, 1/2, 1/3, .... एक ओटोनलिटी भनेको संख्यात्मक कारक (... पहिचान ) द्वारा उत्पन्न पिचहरूको सेट हो ... भाजकमा एक संख्यात्मक स्थिरतामा। विपरित रूपमा, एक Utonality एक Otonality को उल्टो छ, संख्यात्मक कारकहरु मा ... संख्यात्मक कारकहरु माथि संख्यात्मक स्थिर संग पिचहरूको एक सेट।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
अंकगणित पदानुक्रम: गणितीय तर्कमा, अंकगणित पदानुक्रम , अंकगणित पदानुक्रम वा क्लाइन - मोस्तोस्की पदानुक्रम निश्चित सूत्रहरूको परिभाषित गर्ने सूत्रहरूको जटिलताको आधारमा वर्गीकृत गर्दछ। कुनै वर्गीकरण प्राप्त गर्ने कुनै पनि सेटलाई अंकगणित भनिन्छ।
अंकगणित रि ring बीजगणितमा, एउटा कम्युटिभ रिंग आर अंकगणित हो भनिन्छ यदि निम्न कुनै पनि बराबर सर्तहरू राख्छ भने: स्थानीयकरण को आर प्रत्येक अधिकतम आदर्शको लागि एक अis्गालीय ringण हो R को सबै आदर्शका लागि , र , सबै आदर्शका लागि , र ,
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
उल्टो गणित: रिभर्स गणित गणित तर्कको एक प्रोग्राम हो जुन गणितको प्रमेयहरू प्रमाणित गर्न कुन axioms आवश्यक छ निर्धारित गर्न खोज्दछ। यसको परिभाषित विधि संक्षिप्त रूपमा "प्रमेयबाट अज्ञातमा फर्कनु" भनेर वर्णन गर्न सकिन्छ, अज्ञातबाट प्रमेय निकाल्ने सामान्य गणित अभ्यासको विपरित। यो पर्याप्त व्यक्तिहरूबाट आवश्यक सर्तहरू मूर्तिकलाको रूपमा कल्पना गर्न सकिन्छ।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
अंकगणित सेट: गणितीय तर्क मा, एक अंकगणित सेट प्राकृतिक संख्या को एक सेट है कि पेरानो क्रम पहिलो क्रम मा पियानो परिभाषित गर्न सकिन्छ। अंकगणित सेटहरू अंकगणित श्रेणीक्रम द्वारा वर्गीकृत गरीन्छ।
Dedekind zeta प्रकार्य: गणितमा, बीजगणित संख्या फिल्ड K को Dedekind zeta प्रकार्य , सामान्यतया K- s ( हरू ) दर्साउँछ, Riemann zeta प्रकार्यको सामान्यीकरण हो। यसलाई डिरिचलेट श्रृंखलाको रूपमा परिभाषित गर्न सकिन्छ, यससँग युलर उत्पादन विस्तार छ, यसले फंक्शनल इक्वेसनलाई सन्तुष्ट पार्छ, यससँग एउटा विश्लेषणात्मक निरन्तरता छ जटिल प्लेन सीमा मेरुमोर्फिक प्रकार्यको सीधा साधारण पोलको साथ एस = १, र यसको मानहरू इन्कोड हुन्छ। K का अंकगणित डाटा। विस्तारित Riemann परिकल्पना भन्छ कि यदि ζ K ( s ) = 0 र 0 <Re ( s ) <1, तब Re ( s ) = 1/2।
अंकगणित प्रिन्सिपिया, नोवा विधि विस्तार: १ 1889 ise को ग्रन्थ एरिथमेटिक्स प्रिन्सिपिया, ज्युसेप्पे पानाको नोवा मेथोड एक्स्पोजिटा गणितीय तर्क र सेट सिद्धान्तमा एक सेमिनार दस्तावेज हो, जुन अहिले प्राकृतिक संख्याको मानक अडियोमेटाइजेसन भनेको हो, र यसलाई पेनो अक्सिओम्स भनेर चिनिन्छ, साथै केही व्यापक संकेतन, जस्तै। आधारभूत सेट सञ्चालनका लागि प्रतीक रूपमा ∈, ⊂, ∩, ∪, र एक - बी।
अंकगणित प्रिन्सिपिया, नोवा विधि विस्तार: १ 1889 ise को ग्रन्थ एरिथमेटिक्स प्रिन्सिपिया, ज्युसेप्पे पानाको नोवा मेथोड एक्स्पोजिटा गणितीय तर्क र सेट सिद्धान्तमा एक सेमिनार दस्तावेज हो, जुन अहिले प्राकृतिक संख्याको मानक अडियोमेटाइजेसन भनेको हो, र यसलाई पेनो अक्सिओम्स भनेर चिनिन्छ, साथै केही व्यापक संकेतन, जस्तै। आधारभूत सेट सञ्चालनका लागि प्रतीक रूपमा ∈, ⊂, ∩, ∪, र एक - बी।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - थप, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निष्कर्षण। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई आधुनिक गणितको शीर्ष-स्तर विभाजनहरू मध्ये एक मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरूसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
कला को मैदान: रबर्ट रेकर्डको अंकगणित: वा, द ग्राउन्ड अफ आर्ट्स अंकगणितमा छापिएको अंग्रेजी पाठ्यपुस्तकहरु मध्ये एक हो र यो समयको सबैभन्दा लोकप्रिय हो। कलाको ग्राउन्ड अफ आर्ट १ London43 in मा लन्डनमा देखा पर्‍यो र १ 17०० सम्म यसको 45 45 वटा संस्करण पुनः प्रिन्ट गरियो। नयाँ शाखाका सम्पादकहरू र योगदानकर्ताहरू जोन डी, जोन मेलिस, रोबर्ट हार्टवेल, थॉमस विल्सफोर्ड र अन्ततः एडवर्ड ह्याटन थिए।
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
Arithmetico omet ज्यामितीय अनुक्रम: गणितमा, एक अंकगणित – ज्यामितीय अनुक्रम अंकगणितीय प्रगति को संगत सर्तहरूको साथ एक ज्यामितीय प्रगति को अवधि द्वारा अवधि गुणा परिणाम हो। थप सीधै राखे, एक arithmetico-ज्यामितीय अनुक्रम को N औं शब्द को उत्पादन N एक गणित sequenceand को n एक ज्यामितीय एक को औं अवधि को औं अवधि छ। एरिथमेटिको – ज्यामितीय अनुक्रम विभिन्न अनुप्रयोगहरूमा देखा पर्दछ, जस्तै सम्भाव्यता सिद्धान्तमा अपेक्षित मानहरूको गणना। उदाहरण को लागी, अनुक्रम
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - थप, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निष्कर्षण। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई आधुनिक गणितको शीर्ष-स्तर विभाजनहरू मध्ये एक मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरूसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अंकगणित – ज्यामितीय मतलब: गणितमा, अंकगणित – ज्यामितीय माने दुई सकारात्मक वास्तविक संख्या x र y परिभाषित गरिएको छ:
अंकगणित र ज्यामितीय साधनको असमानता: गणितमा, अंकगणित र ज्यामितीय साधनको असमानता , वा अधिक संक्षेपमा एएम – जीएम असमानता , बताउँछ कि गैर-नकारात्मक वास्तविक संख्याहरूको सूचीको अंकगणित माध्य एउटै सूचीको ज्यामितीय मतलब भन्दा ठूलो वा बराबर हो; र अगाडि, ती दुई साधनहरू बराबर छन् र मात्र यदि सूचीमा प्रत्येक संख्या समान छ।
ज्यामितीय मतलब: गणितमा, ज्यामितीय माध्य एक माध्य या औसत हो, जसले केन्द्रीय प्रवृत्ति वा संख्याको सेटको विशिष्ट मानलाई तिनीहरूको मानहरूको उत्पादन प्रयोग गरेर संकेत गर्दछ। Geometric माध्य संख्या 1 एक्स को एक सेट को लागि, N संख्या, अर्थात् को उत्पादन को N औं मूल रूपमा परिभाषित गरिएको छ, एक्स 2, ..., N, geometric माध्य रूपमा परिभाषित गरिएको छ x
अंकगणित तर्क इकाई: कम्प्युटि Inमा, अंकगणित तर्क इकाई (ALU) एक संयुक्त डिजिटल सर्किट हो जुन अंकगणित र बिटवाईज अपरेशन्स पूर्णांक बाइनरी नम्बरहरूमा गर्दछ। यो फ्लोटिंग पोइन्ट एकाइ (FPU) को विपरित हो, जसले फ्लोटिंग पोइन्ट नम्बरहरूमा संचालन गर्दछ। यो कम्प्युटरको केन्द्रीय प्रशोधन इकाई (सीपीयू), FPUs, र ग्राफिक्स प्रोसेसिंग एकाइहरू (GPUs) सहित धेरै प्रकारका कम्प्युटिंग सर्किटहरूको मौलिक भवन ब्लक हो।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - थप, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निष्कर्षण। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई आधुनिक गणितको शीर्ष-स्तर विभाजनहरू मध्ये एक मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरूसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
विश्लेषणको अंकगणित: विश्लेषणको अंकगणित १ th औं शताब्दीको उत्तरार्धमा गरिएको गणितको जगमा अनुसन्धान कार्यक्रम थियो।
विश्लेषणको अंकगणित: विश्लेषणको अंकगणित १ th औं शताब्दीको उत्तरार्धमा गरिएको गणितको जगमा अनुसन्धान कार्यक्रम थियो।
विश्लेषणको अंकगणित: विश्लेषणको अंकगणित १ th औं शताब्दीको उत्तरार्धमा गरिएको गणितको जगमा अनुसन्धान कार्यक्रम थियो।
Geldel को अपूर्णता प्रमेयहरु: Geldel को अपूर्णता प्रमेयहरु गणितीय तर्कको दुई प्रमेयहरु छन् जुन औपचारिक axiomatic सिद्धान्तहरु मा सम्भाव्यताको सीमा संग सम्बन्धित छ। यी नतीजाहरू १ 31 in१ मा कर्ट गुडेलले प्रकाशित गरेका थिए र यो गणितको तर्क र गणितको दर्शनमा महत्वपूर्ण छ। प्रमेय व्यापक रूपमा छन्, तर सर्वव्यापी होइन, यो हिल्बर्टको कार्यक्रम सबै गणितको लागि पूर्ण र एकरूप अक्षहरूको खोज्न असम्भव छ भनेर देखाउँदै व्याख्या गरिएको छ।
Arithmeum: अरिथमेम एक गणित संग्रहालय हो जो फोर्सचung्गसिन्स्टिट फर फर डिक्रेट मैथेमेटिकको बोन विश्वविद्यालयमा छ।
Arithmologia: अरिथमोलोगिया, डेभिटिस न्यूमोरम मिस्टेरिस, जेसुइट विद्वान एथेनासियस किर्चेरले १ 166565 को रचना हो। यो १are औं शताब्दीको मध्यमा रोममा जेसुइट अर्डरका लागि मुख्य प्रिन्टि house घर भरेसे द्वारा प्रकाशित गरिएको थियो। यो फ्रान्ज III लाई समर्पित थियो। नाडास्डी, क्याथोलिक धर्ममा रूपान्तरण गर्ने जसलाई किर्चेरले पहिले Oedipus एजिपियाकस सह-समर्पित गरेका थिए। अरिथोमोलिया भनेको किर्चरको एक मात्र काम हो जुन पूर्ण रूपमा संख्या प्रतीकको विभिन्न पक्षमा समर्पित छ।
संख्या विज्ञान: संख्याशास्त्र भनेको संख्या र एक वा अधिक मिल्दो घटनाहरू बीचको ईश्वरीय वा रहस्यमय सम्बन्धमा विश्वास हो। यो शब्द, नाम, र विचारहरूमा अक्षरहरूको संख्यात्मक मूल्यको अध्ययन पनि हो। यो अक्सर अलौकिक संग सम्बन्धित छ, ज्योतिषको साथ साथै दिव्य कलामा समान।
Rithmomachy: रिथमोमाची एक अत्यधिक जटिल, प्रारम्भिक यूरोपीय गणित बोर्ड खेल हो। यसको प्रारम्भिक ज्ञात विवरण एघारौं शताब्दीको हो। नामको शाब्दिक अनुवाद "नम्बरहरूको युद्ध" हो। खेल धेरै चेस जस्तो छ, क्याप्चरको सबै विधिहरू प्रत्येक टुक्राहरूमा कुँदिएका नम्बरहरूमा निर्भर गर्दछ।
अंकगणित: आधुनिक संख्यावाचक शब्दावलीमा, अंकगणित भनेको कुनै शब्द वा वाक्यांशलाई संख्यात्मक मान दिनमा आधारित ग्रीसको पुरानो isopsephy वा हिब्रू / अरमाईक गेमेट्रियाको सरलीकृत संस्करणको रूपमा ल्याटिन वर्णमालामा रूपान्तरणको आधारमा भविष्यको एक प्रकार हो। अरिथमान्सी कल्दीहरू, प्लेटोनिस्टहरू, पायथागोरियन्स र काबालाहको साथ सम्बन्धित छ। जब कौशलता एक व्यक्तिको नाममा लागू हुन्छ, यो ओमान्मेन्सीको एक रूप हो।
अरिथमोमानिया: अरिथमोमानिया एक मानसिक विकार हो जुन जुन जुनै जुनूनदार – बाध्यकारी डिसअर्डर (ओसीडी) को अभिव्यक्तिको रूपमा देख्न सकिन्छ। यस विकारबाट पीडित व्यक्तिहरूको आफ्नो कार्यहरू वा वस्तुहरू वरपरका ठाउँहरूमा गणना गर्न दृढ आवश्यकता छ।
अरिथमोमानिया: अरिथमोमानिया एक मानसिक विकार हो जुन जुन जुनै जुनूनदार – बाध्यकारी डिसअर्डर (ओसीडी) को अभिव्यक्तिको रूपमा देख्न सकिन्छ। यस विकारबाट पीडित व्यक्तिहरूको आफ्नो कार्यहरू वा वस्तुहरू वरपरका ठाउँहरूमा गणना गर्न दृढ आवश्यकता छ।
अरिथोमिटर: अरिथोमिटर वा अरिथमोमेट्रे पहिलो डिजिटल मेकानिकल क्यालकुलेटर थिए जुन एक अफिस वातावरणमा दैनिक प्रयोग गर्न पर्याप्त पर्याप्त र भरपर्दो थियो। यस क्यालकुलेटरले दुई संख्याहरू सिधै थप्न र घटाउन सक्दछ र परिणामको लागि एक चल संचयीको उपयोग गरेर लामो गुणन र भागहरू प्रभावकारी रूपमा गर्न सक्दछ।
अरिथोमिटर: अरिथोमिटर वा अरिथमोमेट्रे पहिलो डिजिटल मेकानिकल क्यालकुलेटर थिए जुन एक अफिस वातावरणमा दैनिक प्रयोग गर्न पर्याप्त पर्याप्त र भरपर्दो थियो। यस क्यालकुलेटरले दुई संख्याहरू सिधै थप्न र घटाउन सक्दछ र परिणामको लागि एक चल संचयीको उपयोग गरेर लामो गुणन र भागहरू प्रभावकारी रूपमा गर्न सक्दछ।
अरिथोमिटर: अरिथोमिटर वा अरिथमोमेट्रे पहिलो डिजिटल मेकानिकल क्यालकुलेटर थिए जुन एक अफिस वातावरणमा दैनिक प्रयोग गर्न पर्याप्त पर्याप्त र भरपर्दो थियो। यस क्यालकुलेटरले दुई संख्याहरू सिधै थप्न र घटाउन सक्दछ र परिणामको लागि एक चल संचयीको उपयोग गरेर लामो गुणन र भागहरू प्रभावकारी रूपमा गर्न सक्दछ।
न्यूमेरोफोबिया: न्यूमेरोफोबिया , अरिथमोफोबिया वा गणित चिन्ता एक चिन्ता विकार हो, जहाँ अवस्था नम्बर वा गणितको हिसाबले डराउँछ। कहिलेकाँही नम्बरफोबियाले विशेष नम्बरहरूको डरलाई जनाउँदछ।
अंकगणित: आधुनिक संख्यावाचक शब्दावलीमा, अंकगणित भनेको कुनै शब्द वा वाक्यांशलाई संख्यात्मक मान दिनमा आधारित ग्रीसको पुरानो isopsephy वा हिब्रू / अरमाईक गेमेट्रियाको सरलीकृत संस्करणको रूपमा ल्याटिन वर्णमालामा रूपान्तरणको आधारमा भविष्यको एक प्रकार हो। अरिथमान्सी कल्दीहरू, प्लेटोनिस्टहरू, पायथागोरियन्स र काबालाहको साथ सम्बन्धित छ। जब कौशलता एक व्यक्तिको नाममा लागू हुन्छ, यो ओमान्मेन्सीको एक रूप हो।
प्रकाश र छायाको युद्ध: युद्धको प्रकाश र छाया जेनी वर्ट्सको काल्पनिक पुस्तकहरूको श्रृंखला हो। जब पूर्ण हुन्छ, यसले पाँच कहानी आर्कहरू समावेश गर्दछ, पहिलो चार आर्कहरू पूर्णको साथ।
प्रकाश र छायाको युद्ध: युद्धको प्रकाश र छाया जेनी वर्ट्सको काल्पनिक पुस्तकहरूको श्रृंखला हो। जब पूर्ण हुन्छ, यसले पाँच कहानी आर्कहरू समावेश गर्दछ, पहिलो चार आर्कहरू पूर्णको साथ।
प्रकाश र छायाको युद्ध: युद्धको प्रकाश र छाया जेनी वर्ट्सको काल्पनिक पुस्तकहरूको श्रृंखला हो। जब पूर्ण हुन्छ, यसले पाँच कहानी आर्कहरू समावेश गर्दछ, पहिलो चार आर्कहरू पूर्णको साथ।
टाना नदी काउन्टी: टाना रिवर काउन्टी पूर्व तटीय प्रान्त, केन्यामा काउन्टी हो। यो टाना नदी पछि नामाकरण गरिएको छ। यसको क्षेत्रफल, 38,437 square वर्ग किलोमीटर (१,,841१ वर्ग मील) र जनसंख्या 5१5, 43 .43 छ। राजधानी र सबैभन्दा ठूलो शहर होला हो।
Arity: Arity तर्क वा गणित, र कम्प्यूटर विज्ञान मा एक समारोह वा अपरेशन द्वारा लिइएको तर्क वा अपरेट्स को संख्या हो। गणितमा, अरिटीलाई रैंक पनि नाम दिन सकिन्छ, तर यो शब्दले गणितमा अन्य धेरै अर्थहरू राख्न सक्छ। तर्क र दर्शनमा यसलाई आडिसिटि र डिग्री पनि भनिन्छ। भाषाविज्ञानमा यसलाई प्राय: भ्यालेन्सी भनिन्छ ।
कृत्रिम न्यूरल नेटवर्क: कृत्रिम न्यूरल नेटवर्क ( एएनएन ), सामान्यतया केवल न्यूरल नेटवर्कहरू ( एनएन ) भनिन्छ, कम्प्युटि systems प्रणालीहरू अस्पष्ट रूपमा जैविक न्यूरल नेटवर्कहरूद्वारा जनावरको दिमाग गठन गर्ने कम्प्युटर हो।
आर्टेमिस: आर्टेमिस सिकार, मरुभूमि, जंगली जनावरहरू, चन्द्रमा र ईश्वरत्वको ग्रीक देवी हो। देवी डायना उनको रोमन बराबर हो।
अरिन्टिका: अर्निटिका स्ट्रिटोभाल्कानो हो जुन बोलिभियाको सिमाना नजिक चिलीको एरिका वा पेरिनाकोटा क्षेत्रमा छ। यो सालार डी सूयरको उत्तरमा अवस्थित छ। उत्तरमा ज्वालामुखीको मुख्य शिखर, केही छोटो दक्षिणी शिखर र पश्चिममा सहायक शिखर छ। एक हिमनदी उपत्यका शिखर बीच छ। हिमरेखाको उचाई ,,5 meters ० मिटर (१,,340० फिट) छ। अर्निटिकामा फेला परेको दोस्रो मोरेनको दक्षिणी भागमा ,,350० मिटर (१,,२70० फिट) देखि पूर्वी मैदानमा ,,5 meters० मिटर (१,, 30 30० फिट) को उचाइ छ। पश्चिमी भागमा तिनीहरू ,,०० मिटर (१,,4०० फिट) को उचाईमा पुग्छन्। कुलमा, पाँच हिमनदीहरूले अरिन्टिकालाई घेरा हाले र सालार डि सुरेरमा ओर्ले। हाल, रक हिमनदीहरू पहाडमा सक्रिय छन्।
Arritinngithigh भाषा: अरिटिंng्गी एक अष्ट्रेलियाली आदिवासी भाषा हो जुन एकपटक क्वीन्सल्याण्डको केप योर्कमा बोलिन्छ।
Arritinngithigh भाषा: अरिटिंng्गी एक अष्ट्रेलियाली आदिवासी भाषा हो जुन एकपटक क्वीन्सल्याण्डको केप योर्कमा बोलिन्छ।
Arritinngithigh भाषा: अरिटिंng्गी एक अष्ट्रेलियाली आदिवासी भाषा हो जुन एकपटक क्वीन्सल्याण्डको केप योर्कमा बोलिन्छ।
Arritinngithigh भाषा: अरिटिंng्गी एक अष्ट्रेलियाली आदिवासी भाषा हो जुन एकपटक क्वीन्सल्याण्डको केप योर्कमा बोलिन्छ।
रमिल अरितकुलोभ: रमिल कमिलेविच अरितकुलोभ एक रूसी मध्य दूरीका धावक हुन् जसले 800०० मिटरमा विशेषज्ञता प्राप्त गर्छन्।
एसके अरिटमा प्राग: एसके अरिटमा प्राग चेक फुटबल क्लब हो जुन प्राग-भोकोभिसमा अवस्थित छ। यो हाल चेक चौथो डिभिजन मा खेल्छ।
एसके अरिटमा प्राग: एसके अरिटमा प्राग चेक फुटबल क्लब हो जुन प्राग-भोकोभिसमा अवस्थित छ। यो हाल चेक चौथो डिभिजन मा खेल्छ।
अंकगणित: अंकगणित गणितको एक शाखा हो जसले संख्याहरूको अध्ययन समावेश गर्दछ, विशेष गरी उनीहरूमा परम्परागत अपरेशनको सम्पत्तीको सम्बन्धमा - थप, घटाउ, गुणन, भाग, एक्सपोन्टेनेसन र जराको निष्कर्षण। अंकगणित संख्याको सिद्धान्तको एक प्राथमिक अंश हो, र संख्या सिद्धान्तलाई आधुनिक गणितको शीर्ष-स्तर विभाजनहरू मध्ये एक मानिन्छ, बीजगणित, ज्यामिति र विश्लेषणको साथ। अंकगणित र उच्च अंकगणित शब्द २० औं शताब्दीको शुरूसम्म संख्या सिद्धान्तको पर्यायवाचीको रूपमा प्रयोग गरिन्थ्यो र कहिलेकाँही अझै पनि संख्या सिद्धान्तको एक विस्तृत भागलाई जनाउन प्रयोग गरिन्थ्यो।
अरितमिजा: Aritmija उल्लेख गर्न सक्नुहुन्छ: अरितमिजा (उपन्यास) , २०० 2004 का उपन्यास स्लोभेनियाली लेखक जानी भिर्क अरितमिजा (एल्बम) , २०० 2006 एल्बम क्रोएशियन ब्यान्ड भात्रा द्वारा
अरितमिजा: Aritmija उल्लेख गर्न सक्नुहुन्छ: अरितमिजा (उपन्यास) , २०० 2004 का उपन्यास स्लोभेनियाली लेखक जानी भिर्क अरितमिजा (एल्बम) , २०० 2006 एल्बम क्रोएशियन ब्यान्ड भात्रा द्वारा
अरितमिजा (उपन्यास): अरितमिजा स्लोभेनियाली लेखक जानी भिर्कको उपन्यास हो। यो पहिलो पटक २०० 2004 मा प्रकाशित भएको थियो।
मिचियो अरिटो: मिचियो एरिटो निप्पॉन प्रोफेशनल बेसबलमा जापानी पूर्व पेशेवर बेसबल तेस्रो बेसम्यान हो। उनले १ 69। To देखि १ 6 .6 सम्म लोटे ओरियनहरूको लागि आफ्नो सम्पूर्ण क्यारियर खेले। उनी १ 69। In मा प्यासिफिक लिग रुकी अफ द इयर थिए।
Arito स्टेशन: Arito स्टेशन पूर्वी जापान रेलवे कम्पनी द्वारा संचालित जापानको अओमोरी प्रान्त, कामिकिता जिल्ला नोहेजी शहरको एक रेलवे स्टेशन हो।
एरिटोमो: Aritomo एक मर्दाना जापानी दिइएको नाम हो। नामको साथ उल्लेखनीय व्यक्तिहरू समावेश गर्दछ: एरिटोमो गोटी , इम्पीरियल जापानी नेवी एडमिरल यामगाता अरिटोमो , जापानी सामान्य र जापानका प्रधानमन्त्री
एरिटोमो गोटी: एरिटोमो गोटी दोस्रो विश्वयुद्धको बेला इम्पीरियल जापानी नेवीमा एडमिरल थिए।
एरिटोमो गोटी: एरिटोमो गोटी दोस्रो विश्वयुद्धको बेला इम्पीरियल जापानी नेवीमा एडमिरल थिए।
यामगाता अरिटोमो: गेन्सुई प्रिन्स यामागाता अरिटोमो जसलाई प्रिन्स यामागाता क्युसुके पनि भनिन्छ, उनी एक वरिष्ठ र ranking ्गेली जापानी सैन्य कमाण्डर थिए, जापानका दुई पटक निर्वाचित प्रधानमन्त्री थिए, र जेनेरीका एक अग्रणी सदस्य थिए, जुन वरिष्ठ राजनैतिक समूहको अग्लो समूह थियो जसले मेइजी बहाली पछि जापानमा प्रभुत्व जमाए। इम्पीरियल जापानी सेनाको उद्घाटन चीफ अफ स्टाफको रूपमा उनी जापानको सैन्य साम्राज्यको साम्राज्य र यसको प्रतिक्रियावादी विचारधाराको मुख्य वास्तुकार थिए। यस कारणले, केही इतिहासकारहरू यामगातालाई जापानी सैन्यवादको "पिता" मान्छन्।
एरिटन, अलाबामा: एरिटन डेल काउन्टी, अलाबामा, संयुक्त राज्य अमेरिका मा एक शहर हो। २०१० को जनगणनामा जनसंख्या 646464 थियो। यो अप्रिल १ 190 ०6 मा समाहित भएको थियो। नाम यसको दुई पूर्ववर्ती शहर नामहरू: एरि ओस्टो र चार्ल टोनको मिश्रण हो।
एरिटन, अलाबामा: एरिटन डेल काउन्टी, अलाबामा, संयुक्त राज्य अमेरिका मा एक शहर हो। २०१० को जनगणनामा जनसंख्या 646464 थियो। यो अप्रिल १ 190 ०6 मा समाहित भएको थियो। नाम यसको दुई पूर्ववर्ती शहर नामहरू: एरि ओस्टो र चार्ल टोनको मिश्रण हो।
एरिटन, अलाबामा: एरिटन डेल काउन्टी, अलाबामा, संयुक्त राज्य अमेरिका मा एक शहर हो। २०१० को जनगणनामा जनसंख्या 646464 थियो। यो अप्रिल १ 190 ०6 मा समाहित भएको थियो। नाम यसको दुई पूर्ववर्ती शहर नामहरू: एरि ओस्टो र चार्ल टोनको मिश्रण हो।
एरिटन, अलाबामा: एरिटन डेल काउन्टी, अलाबामा, संयुक्त राज्य अमेरिका मा एक शहर हो। २०१० को जनगणनामा जनसंख्या 646464 थियो। यो अप्रिल १ 190 ०6 मा समाहित भएको थियो। नाम यसको दुई पूर्ववर्ती शहर नामहरू: एरि ओस्टो र चार्ल टोनको मिश्रण हो।
Aritox: अरिटोक्स शब्द मोनोक्लोनल एन्टिबडीको नाममा देखा पर्दछ र तिनीहरू रेखिन प्रोटीनको श्रृंखलामा जोडिएको छ भनेर संकेत गर्दछ। Telimomab aritox Zolimomab aritox
Zolimomab aritox: Zolimomab aritox एक माउस मोनोक्लोनल एन्टिबडी हो जुन प्रणालीगत लुपुस एरिथेमाटोसस र ग्रफ्ट-बनाम-होस्ट रोगको उपचारको लागि अनुसन्धान गरिएको थियो, तर अध्ययनले औषधिको सकारात्मक प्रभाव देखाउन असफल भयो।
अरित्रा: अरित्रा एक भारतीय पुरुषत्वको नाम हो। नामको साथ उल्लेखनीय व्यक्तिहरू समावेश गर्दछ: अरित्रा दत्ता बनिक, बंगाली फिल्म अभिनेता अरित्रा दत्ता, सिंगापुरका क्रिकेटर
क्रमबद्ध मोशन तस्वीरहरु: असार्टेड मोशन पिक्चर्स एक उत्पादन घर हो जुन मुम्बई, भारतमा आधारित छ। यो घर २rit अगस्ट २०१ 2015 मा अरित्रा दास, सर्बनी मुखर्जी र राम कमल मुखर्जीले स्थापना गरेका थिए।
अरित्रा दत्ता: अरित्रा दत्ता सिंगापुरका क्रिकेटर हुन्। अक्टुबर २०१ he मा, उनी ओमानमा २०१ ICC आईसीसी विश्व क्रिकेट लिग डिभिजन तीन प्रतियोगिताको लागि सिंगापुरको टीममा नामित भए। उनले १० नोभेम्बर २०१ on मा ओमानको बिरूद्ध सिंगापुरको ओपनिंग टूर्नामेन्टमा खेले। टुर्नामेन्टमा उनी सिंगापुरका लागि सर्वाधिक रन बनाए। पाँच खेलमा २० 20 रन बनाए।